Metadata

This post will not make any sense without first reading my previous post on Visualising Homomorphisms where I explain the visual intuitions I'll be using here.

So to start off, the theorems:

Schreier Refinement Theorem

Let $\Sigma_G$ and $\Sigma_H$ be subnormal series of a group $G$. Then one can construct two subnormal series $\Sigma_G'$ and $\Sigma_H'$ with the same multiset of factor groups such that $\Sigma_G'$ contains $\Sigma_G$ and $\Sigma_H'$ contains $\Sigma_H$. I use $\Sigma_X'$ contains $\Sigma_X$ to mean that all the subgroups in $\Sigma_X$ are also in $\Sigma_X'$. It is in this sense that $\Sigma_X'$ is a “finer slicing” (informal) of group $G$ than $\Sigma_X$.

Jordan-Hölder Theorem

Let $G$ be a finite group where $G \ne 1$. Then $G$ has a composition series. While said composition series isn't unique in general, the composition factors of any two composition series of $G$ have the same multiset of composition factors.

Now, a typical way to prove the Jordan-Hölder Theorem is to show that it is an easy consequence of the Schreier Refinement Theorem, which is proved via repeated applications of the Butterfly Lemma. Given how relatively symbol heavy the Butterfly Lemma is, the proof of the Schreier Refinement Theorem is often full of indices and symbols and such.

Here, I'll first be giving an informal visual proof followed by a some justifications missing in the informal proof. The informal visual proof shows that, in some sense, both the Schreier Refinement Theorem and Jordan-Hölder Theorem are “obvious”, and the visual intuition also illustrates the motivations behind the machinary of the proofs one would see of these theorems.

(Informal) Visual Proof

Schreier Refinement Theorem

Let $\Sigma_G$ and $\Sigma_H$ be two subnormal series of $G$:

\[\Sigma_G: 1 = G_0 \trianglelefteq G_1 \trianglelefteq G_2 \trianglelefteq \cdots \trianglelefteq G_n = G \\ \Sigma_H: 1 = H_0 \trianglelefteq H_1 \trianglelefteq H_2 \trianglelefteq \cdots \trianglelefteq H_m = G\]

We can visually represent this as such. Note I've take $n = 3$ and $m=4$ for the visual.

One can immediately see that $G$ can be split into the factor groups $X_{i,j}$ where $1 \le i \le n$ and $ 1\le j \le m$. These factor groups $X_{i,j}$ in turn also split the factor groups of $\Sigma_G$ and $\Sigma_H$.

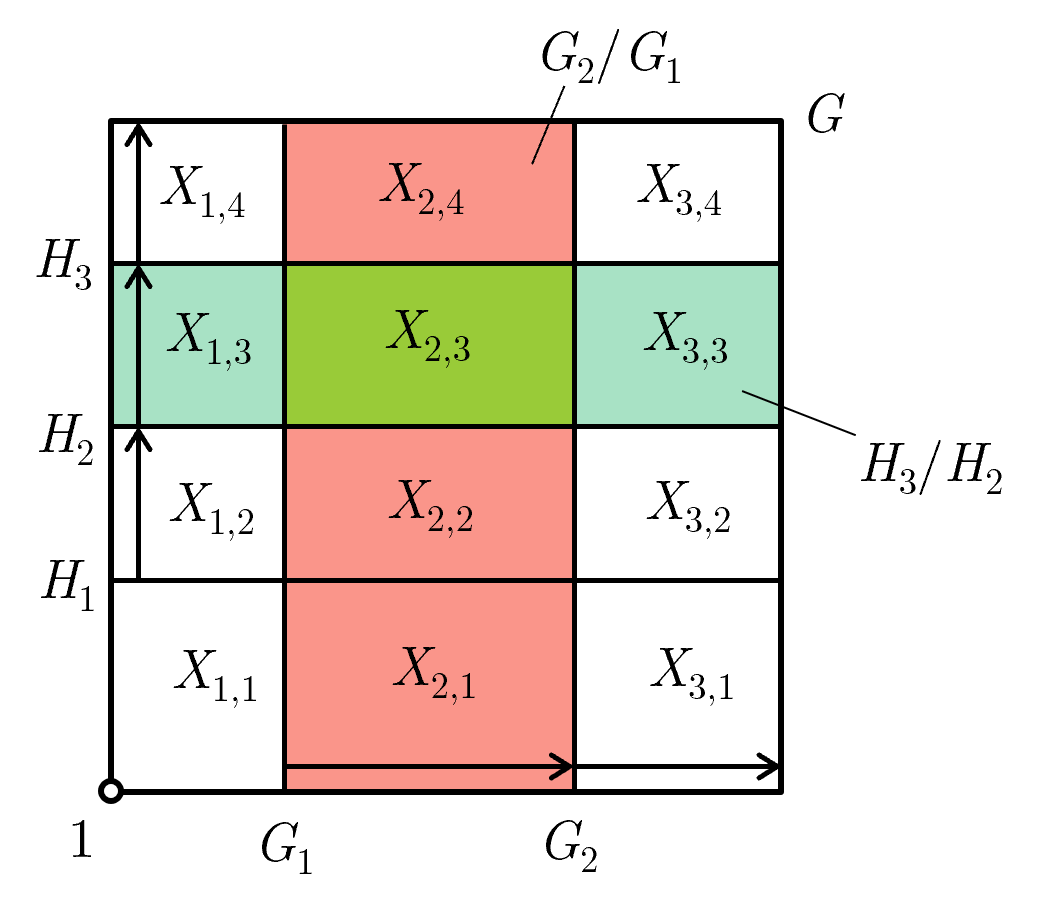
Now can we construct subnormal series $\Sigma_G'$ and $\Sigma_H'$ that has $X_{i,j}$ as their factor groups, such that $\Sigma_G$ and $\Sigma_H$ are contained in $\Sigma_G'$ and $\Sigma_H'$ respectively (hence proving the theorem)?

Well visually, we can see two ways to describe the factor group $X_{i,j}$:

1. $G_{i-1} (G_i \cap H_j) \;/\; G_{i-1} (G_i \cap H_{j-1})$
2. $H_{j-1} (H_j \cap G_i) \;/\; H_{j-1} (H_j \cap G_{i-1})$

We can hence define two sequences which involves starting from $1$ and iteratively appending more $X_{i,j}$ factor groups both column-wise and row-wise respectively until we reach $G$. Appending column-wise we get $\Sigma_G'$ which contains $\Sigma_G$, and appending row-wise we get $\Sigma_H'$ which contains $\Sigma_H$.

\[\begin{aligned} &\Sigma_G' = \{\\ & &1 = G_0 = &\;G_0 (G_1 \cap H_0)\trianglelefteq\\ & &&\;G_0 (G_1 \cap H_1)\trianglelefteq G_0 (G_1 \cap H_2)\trianglelefteq \cdots\trianglelefteq \\ & &G_1 = &\;G_0 (G_1 \cap H_m)\trianglelefteq\\ & &&\;G_1 (G_2 \cap H_1)\trianglelefteq G_1 (G_2 \cap H_2)\trianglelefteq \cdots\trianglelefteq \\ & &G_2 = &\;G_1 (G_2 \cap H_m)\trianglelefteq\\ & &&\cdots\trianglelefteq \\ & &G = G_n = &\;G_{n-1} (G_n \cap H_m)\\ &\} \\ \\ &\Sigma_H' = \{\\ & &1 = H_0 = &\;H_0 (H_1 \cap G_0)\trianglelefteq\\ & &&\;H_0 (H_1 \cap G_1)\trianglelefteq H_0 (H_1 \cap G_2)\trianglelefteq \cdots\trianglelefteq \\ & &H_1 = &\;H_0 (H_1 \cap G_n)\trianglelefteq\\ & &&\;H_1 (H_2 \cap G_1)\trianglelefteq H_1 (H_2 \cap G_2)\trianglelefteq \cdots\trianglelefteq \\ & &H_2 = &\;H_1 (H_2 \cap G_n)\trianglelefteq\\ & &&\cdots\trianglelefteq \\ & &G = H_m = &\;H_{m-1} (H_m \cap G_n)\\ &\} \\ \end{aligned}\]

Here is $\Sigma_G'$ and $\Sigma_H'$ as an animation:

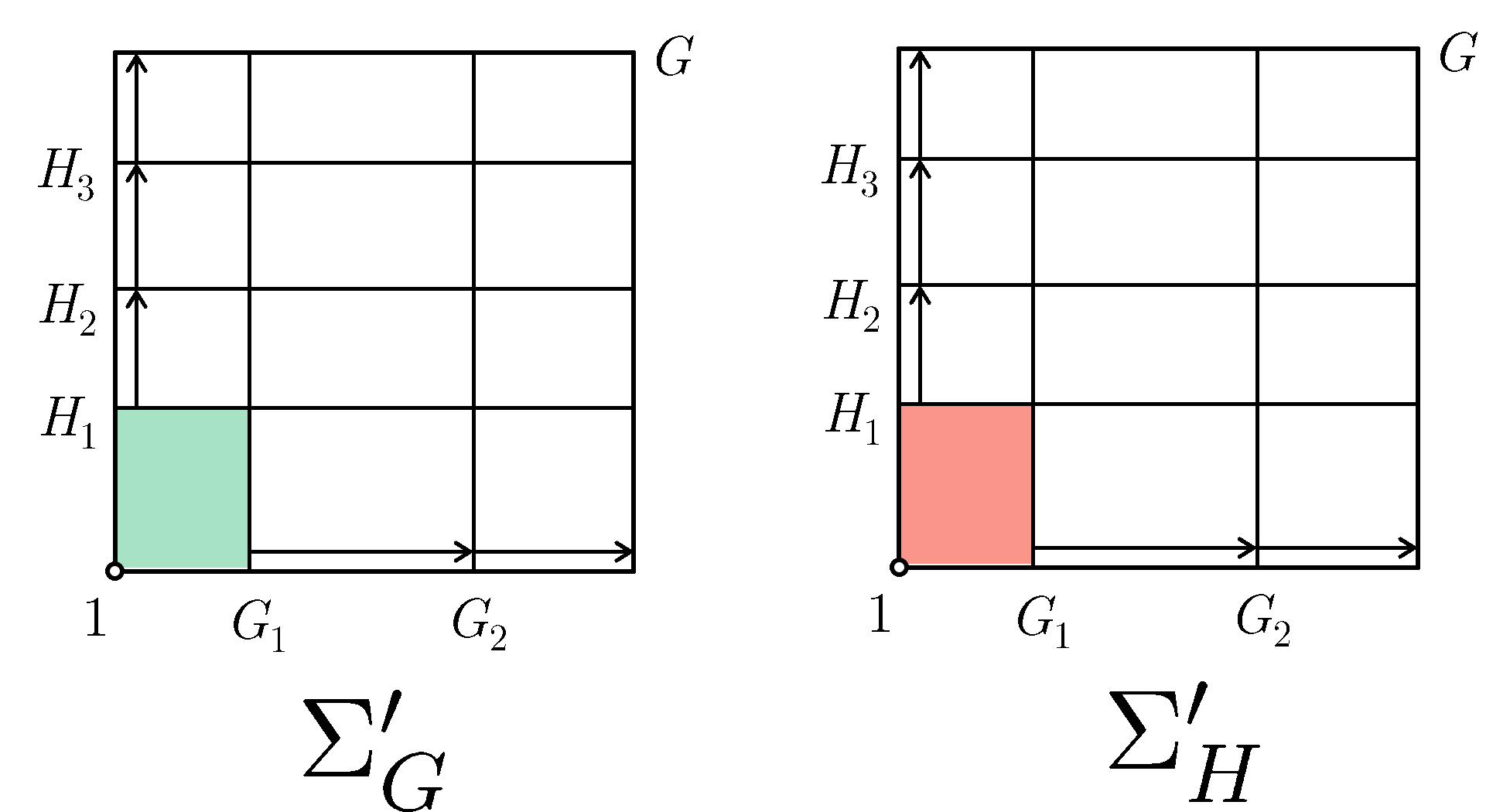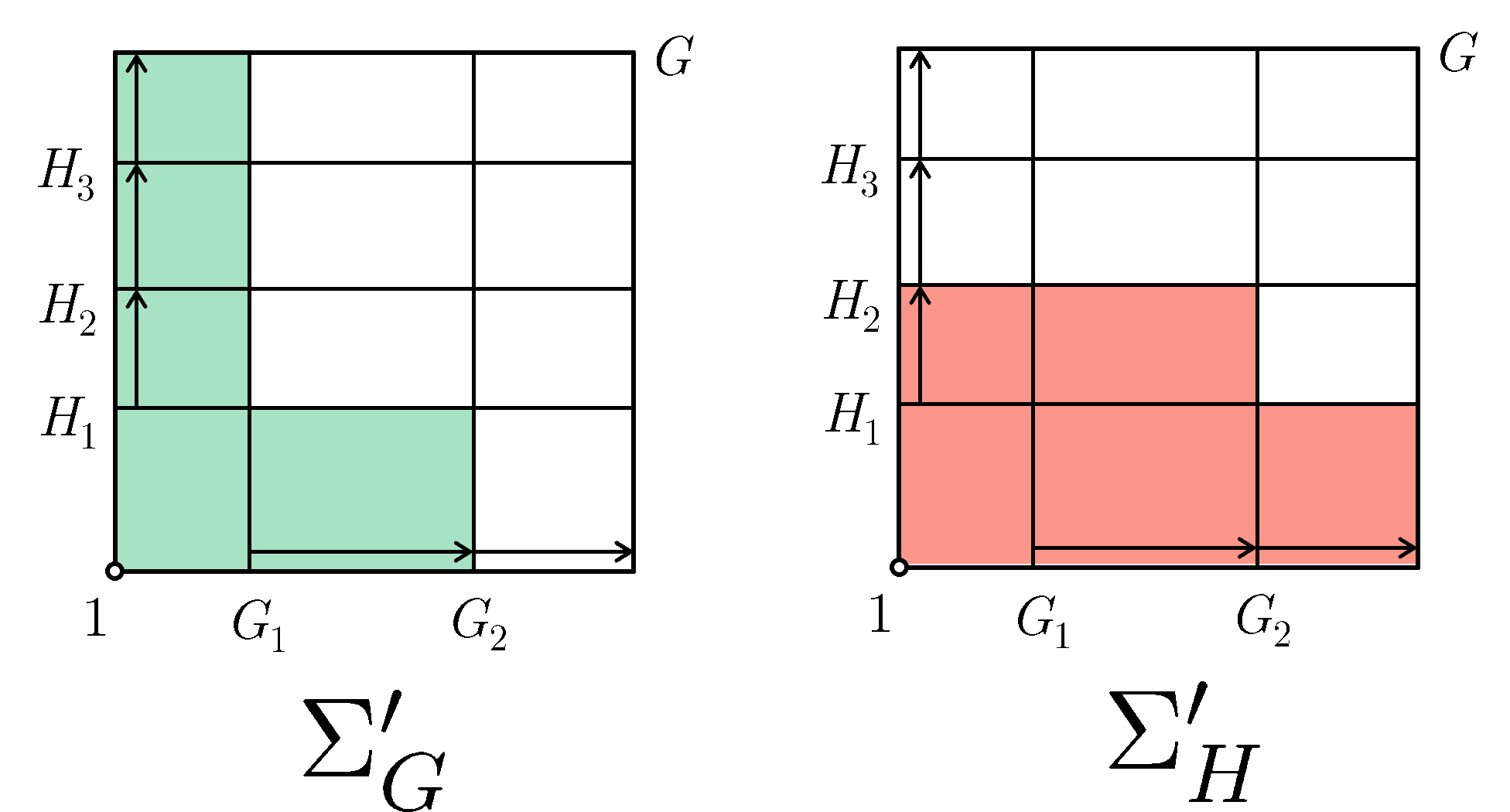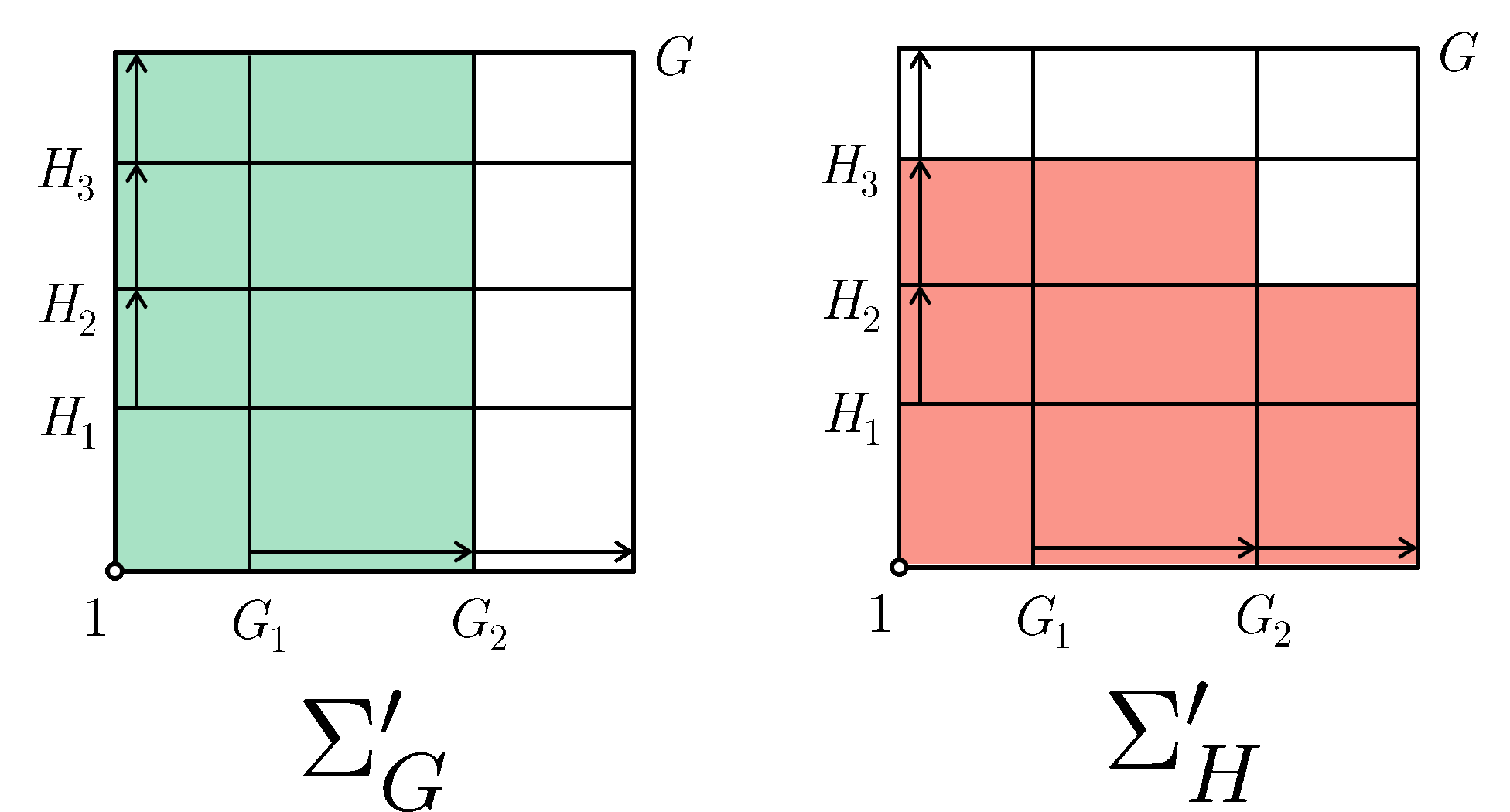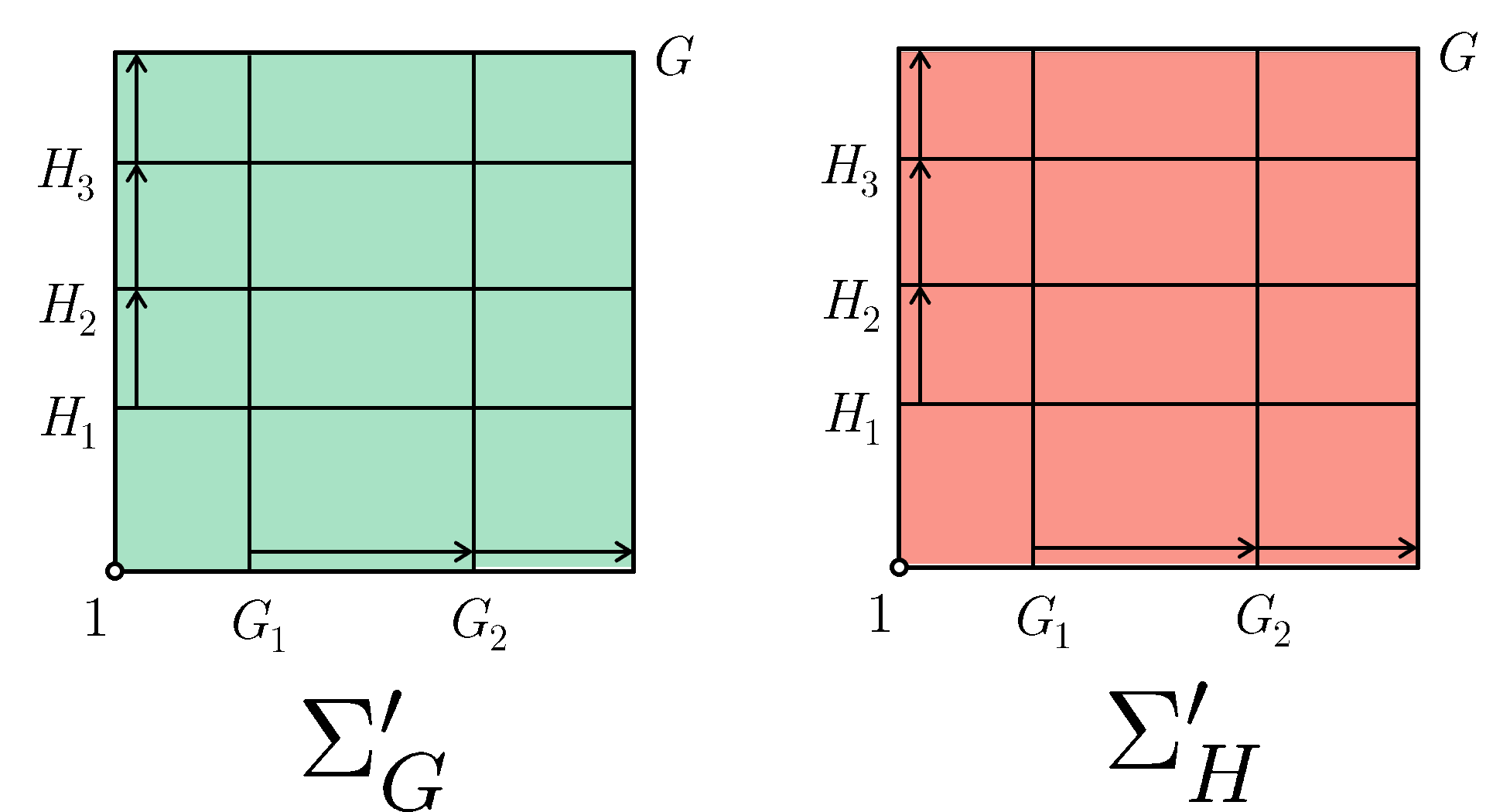
Visually it is obvious that both $\Sigma_G'$ and $\Sigma_H'$ contains $\Sigma_G$ and $\Sigma_H$ respectively, and both have $X_{i,j}$ as their factor groups.

Jordan-Hölder Theorem

Now suppose instead of just subnormal series $\Sigma_G$ and $\Sigma_H$ of $G$, we have $\Sigma_G$ and $\Sigma_H$ be composition series. Informally, this means each factor group of $\Sigma_G$ and $\Sigma_H$ is simple and hence cannot be “sliced further”. This means our $X_{i,j}$ factor groups must be equal, up to permutation, to the factor groups of $\Sigma_G$ (and of $\Sigma_H$), after removing trivial factor groups ($X_{i,j} = 1$). Hence the constructed series $\Sigma_G'$ and $\Sigma_H'$ will have duplicates, and after removing those duplicates we must have $\Sigma_G' = \Sigma_G$ and $\Sigma_H' = \Sigma_H$. Since $\Sigma_G'$ and $\Sigma_H'$ have the same factor groups up till permutation, we can say the same thing for $\Sigma_G$ and $\Sigma_H$. Done.

Visually, suppose we have the factor group $G_3/G_2$ be simple and hence cannot be sliced further. Then we must have $X_{3,1}$, $X_{3,2}$, $X_{3,3}$, $X_{3,4}$ be isomorphic to either $1$ or $G_3/G_2$, which can be represented visually as such:

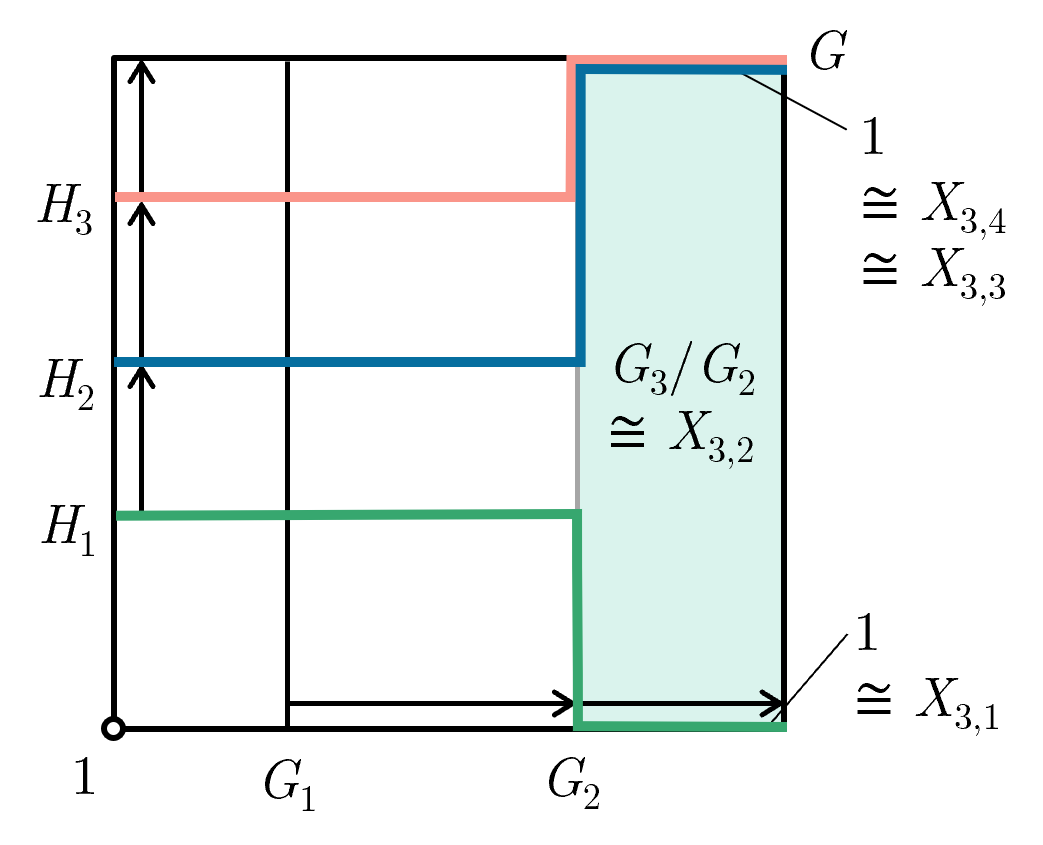
This visually explains why some $X_{i,j}$ will be trivial.

Justifications

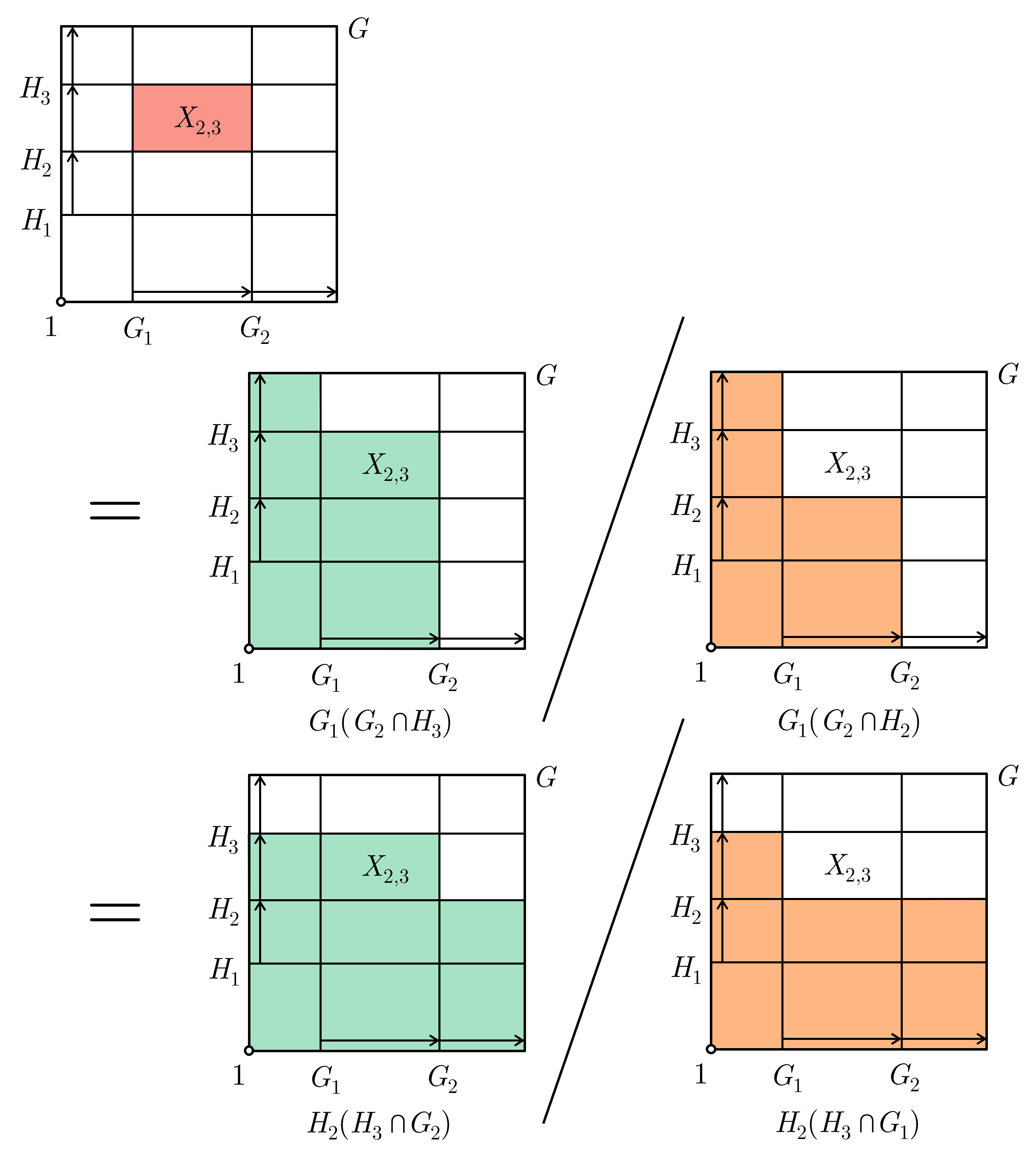
We have shown visually that the factor group $X_{i,j}$ can be given as:

1. $G_{i-1} (G_i \cap H_j) \;/\; G_{i-1} (G_i \cap H_{j-1})$
2. $H_{j-1} (H_j \cap G_i) \;/\; H_{j-1} (H_j \cap G_{i-1})$

but we still need to justify that they are isomorphic.

I refer to the above image and to the butterfly lemma visual in my previous post. Both images do look really similar doesn't it? That's because we can apply the Butterfly Lemma to the tuple $(A,B,C,D) = (G_i, G_{i-1}, H_j, H_{j-1})$, which is justified as $G_{i-1} \trianglelefteq G_i$ and $H_{j-1} \trianglelefteq H_j$.

The butterfly lemma also shows that the factor groups $X_{i,j}$ are well-defined, as we've also shown that $G_{i-1} (G_i \cap H_{j-1}) \trianglelefteq G_{i-1} (G_i \cap H_j)$ and $H_{j-1} (H_j \cap G_{i-1}) \trianglelefteq H_{j-1} (H_j \cap G_i)$