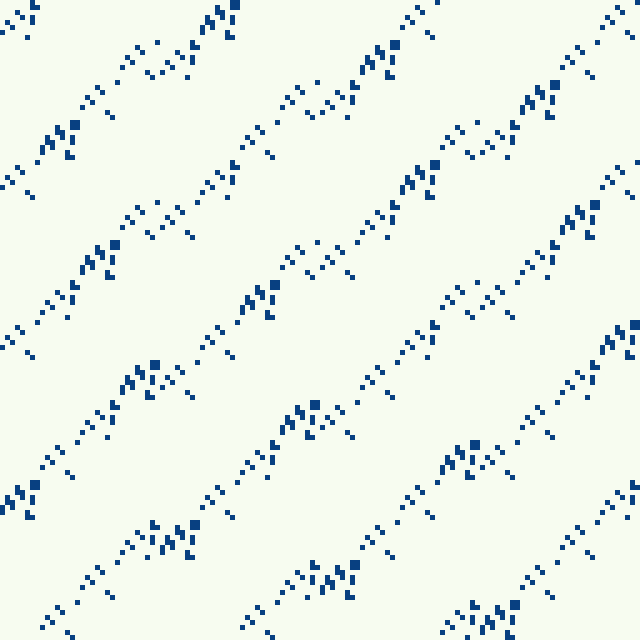
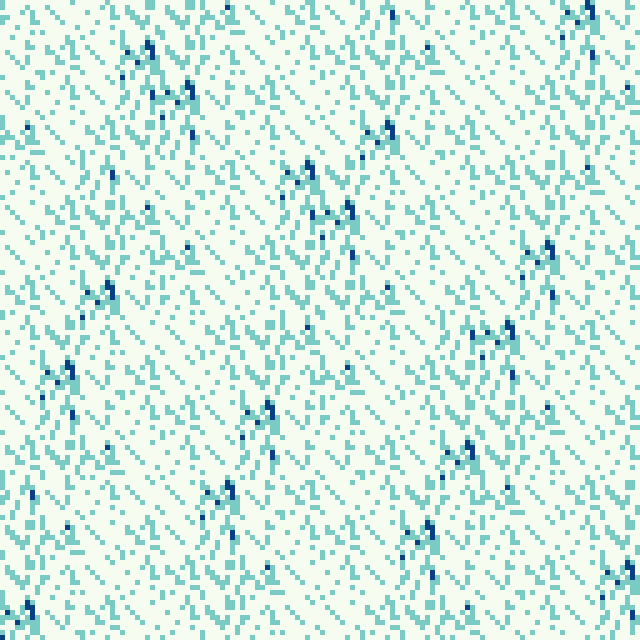
AES-128 Diffusion
Gallery
Plot of diffusion for round 0 to 8. You can see the plot getting more and more random as the number of rounds increase.
Plot of diffusion for round 0.
Plot of diffusion for round 1.
Plot of diffusion for round 2.
Plot of diffusion for round 3.
Plot of diffusion for round 4.
Plot of diffusion for round 5.
Plot of diffusion for round 6.
Plot of diffusion for round 7.
Plot of diffusion for round 8.
Plot of diffusion for round 9.
Plot of diffusion for round 10.
Metadata
I made this originally to be displayed in the Seattle Universal Math Museum, “For the Love of Math!” exhibition curated by Timea Tihanyi, but for reasons I forgot I decided against it and submitted MT19937 instead.
I revisited this today and realised wait hey this is interesting, and made the plots more visually appealing.
What is AES?
So AES is a symmetric-key encryption algorithm. It works by shuffling (unrigorous definition) the plaintext bits around to create the ciphertext. AES-128 is a specific instance of AES that works on $128$ bits of plaintext at a time, in order words, AES-128 has a 128-bit state.
AES is mostly linear in $GF(2)$. It consists of multiple rounds of the following operations:
- Substitute
- Shift
- Mix
- Add round key
In particular, steps 2-4 are linear operations, and can be represented as a matrix. Step 1 (Substitute) however, isn't linear, and cannot be represented as a matrix. Needless to say, the Substitute step is one of the biggest reasons that AES is so hard to break.
What am I plotting?
Each plot represents the “dependencies” of each input bit at each round of AES. The plot for round 0 is the identity matrix, as each bit only depends on itself.
At subsequent rounds, the “dependencies” of each output bit becomes entangled with more and more input bits, resulting in a random plot at the later rounds. This is known as diffusion, and is very important in cryptography.
The Substitute operation is dealt probabilistically, as for a given $n$-th bit, even knowing its value before Substutite, can result in both $0,1$ after Substitute, because this operation is done at the byte level. The Substitute operation is responsible for most of the colour variations of this collection of images.
I also did other stuff that's not as faithful to the original AES-128 such as switching to the field $\mathbb{Z}$ in gen_n_rounds because it gives more visually interesting results. The final plots, however, are still faithful to what I'm trying to visualize.
Code
Sage:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
from sage.all import *
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
aes = mq.SR(10, 4, 4, 8, star=True, allow_zero_inversions=True)
F = aes.base_ring()
FP = PolynomialRing(F, 'k', 16)
key = FP.gens()
init_state = matrix(FP, [list(key[4*i:4*i+4]) for i in range(4)])
x = F.gens()[0]
def state_nth_bit(n:int):
s = [list(i) for i in aes.state_array()]
nb = n >> 3
s[nb >> 2][nb & 3] = x^(n%8)
return s
def flatten_aes_state(s):
s = [j for i in s for j in list(i)]
s = [i.polynomial().exponents() for i in s]
s = [int(i in j) for j in s for i in range(8)]
return s
def get_mix_mat_GF2():
mats = []
for i in range(16*8):
mats.append(aes.mix_columns(state_nth_bit(i)))
return matrix(ZZ, [flatten_aes_state(m) for m in mats]).T
sbox = aes.sbox()
def get_prob_bit(n:int):
prob = [0]*8
for i in range(0x100):
if (i>>n) & 1 == 0:
continue
sb = sbox[i]
for j in range(8):
if (sb>>j) & 1:
prob[j] += 1
return prob
shuf = list(range(8))
def get_prob_bit(n:int):
prob = [0]*8
prob[shuf[n]] = 1
return prob
def get_sub_mat_GF2():
sub_mat = np.array([get_prob_bit(i) for i in range(8)], dtype=int)
sub_mat = (sub_mat - sub_mat.min()) / (sub_mat.max() - sub_mat.min())
sub_mat = matrix(ZZ, sub_mat.astype(int)).T
return block_diagonal_matrix(*tuple([sub_mat]*16))
shift = matrix(ZZ, aes.shift_rows_matrix())
mix = get_mix_mat_GF2()
sub = get_sub_mat_GF2()
def gen_n_rounds(n:int):
r1 = identity_matrix(ZZ, 128)
for i in range(n):
r1 = sub*r1
r1 = shift*r1
r1 = mix*r1
return r1
n = 3
scale = 5
sz = 128*n*scale
cmap = plt.get_cmap('GnBu')
fimg = np.zeros((sz,sz,4), dtype=np.uint8)
for i in range(n*n):
r1 = gen_n_rounds(i)
y,x = i%n, i//n
r1 = np.array(r1, dtype=float)
r1 = (r1 - r1.min())/(r1.max() - r1.min())
img = np.kron(r1, np.ones((scale,scale)))
img = (cmap(img)*255).astype(np.uint8)
fimg[
128*scale*x:128*scale*(x+1),
128*scale*y:128*scale*(y+1)
] = img
img = Image.fromarray(fimg)
img.save("dist/aes128-diffusion-9r-mod128.png")
for i in range(11):
r1 = gen_n_rounds(i)
r1 = np.array(r1, dtype=float)
r1 = (r1 - r1.min())/(r1.max() - r1.min())
img = np.kron(r1, np.ones((scale,scale)))
img = (cmap(img)*255).astype(np.uint8)
Image.fromarray(img).save(f"dist/aes128-diffusion-9r-mod128-{i}.png")