Metadata

Competition: SEETF 2022
Date: (Sat) 4 June 0000hrs - (Mon) 6 June 0000hrs (SGT, 48 Hours)
Challenge Source: Social-Engineering-Experts/SEETF-2022-Public

So I was invited to write challenges for SEETF 2022 and had a lot of fun writing the challenges and spectating the competition. It is a joy working with the SEE team.

The number of competition signups exceeded way beyond my expectations. A total of 1221 registered, and judging by the number of teams that solved at least one challenge, at least 500 teams participated.

This CTF is also twice the scale as per usual, with over 50 challenges to occupy 48 hours, with 14 challenges aimed at being beginner friendly. Considering 12/14 of those challenges hit >50 solves, I'd say we quite successfully identified challenges that are accessible to newcomers yet still pose a considerable challenge. Good job on all new teams that solved at least 1 beginner friendly challenge! Hope you've learnt something!

The True ECC

Category: Crypto
Intended Difficulty: Medium
Solved: 20
Points: 871
Flag: SEE{W4it_whaT_do_y0u_meaN_Ecc_d0esnt_Us3_e1Lipses}

You know what you think of when you hear “Elliptic Curve”? It's ellipses of course!

The challenge implements Diffie–Hellman key exchange key exchange on a group defined as points $(x,y)$ on the ellipse $x^2 + ay^2 = 1 \mod p$, $a = 376014, \; p = 2^{512} - 1$. Point addition in defined as $(x,y) + (w,z) = (xw - ayz, xz + yw)$, which combines two points on the ellipse into a new point on the ellipse.

We are given alice's and blake's public key and the ciphertext, and we're asked to recover the plaintext (flag).

See DLP implementation:

# python ecc.py > out.py

from random import randint
from os import urandom
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from hashlib import sha1

from typing import Tuple


class Ellipse:

    """Represents the curve x^2 + ay^2 = 1 mod p"""

    def __init__(self, a: int, p: int):

        self.a = a
        self.p = p

    def __repr__(self) -> str:
        return f"x^2 + {self.a}y^2 = 1 mod {self.p}"

    def __eq__(self, other: 'Ellipse') -> bool:
        return self.a == other.a and self.p == other.p

    def is_on_curve(self, pt: 'Point') -> bool:

        x, y = pt.x, pt.y
        a, p = self.a, self.p
        return (x*x + a * y*y) % p == 1


class Point:

    """Represents a point on curve"""

    def __init__(self, curve: Ellipse, x: int, y: int):

        self.x = x
        self.y = y
        self.curve = curve
        assert self.curve.is_on_curve(self)

    def __repr__(self) -> str:
        return f"({self.x}, {self.y})"

    def __add__(self, other: 'Point') -> 'Point':

        x, y = self.x, self.y
        w, z = other.x, other.y
        a, p = self.curve.a, self.curve.p

        nx = (x*w - a*y*z) % p
        ny = (x*z + y*w) % p
        return Point(self.curve, nx, ny)

    def __mul__(self, n: int) -> 'Point':

        assert n > 0

        Q = Point(self.curve, 1, 0)
        while n > 0:
            if n & 1 == 1:
                Q += self
            self += self
            n = n//2
        return Q

    def __eq__(self, other: 'Point') -> bool:
        return self.x == other.x and self.y == other.y


def gen_secret(G: Point) -> Tuple[Point, int]:

    priv = randint(1, p)
    pub = G*priv
    return pub, priv


def encrypt(shared: Point, pt: bytes) -> bytes:

    key = sha1(str(shared).encode()).digest()[:16]
    iv = urandom(16)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ct = cipher.encrypt(pad(pt, 16))
    return iv + ct


def decrypt(shared: Point, ct: bytes) -> bytes:

    iv, ct = ct[:16], ct[16:]
    key = sha1(str(shared).encode()).digest()[:16]
    cipher = AES.new(key, AES.MODE_CBC, iv)
    pt = cipher.decrypt(ct)
    return unpad(pt, 16)


a, p = 376014, (1 << 521) - 1
curve = Ellipse(a, p)

gx = 0x1bcfc82fca1e29598bd932fc4b8c573265e055795ba7d68ca3985a78bb57237b9ca042ab545a66b352655a10b4f60785ba308b060d9b7df2a651ca94eeb63b86fdb
gy = 0xca00d73e3d1570e6c63b506520c4fcc0151130a7f655b0d15ae3227423f304e1f7ffa73198f306d67a24c142b23f72adac5f166da5df68b669bbfda9fb4ef15f8e
G = Point(curve, gx, gy)

if __name__ == "__main__":

    from flag import flag

    alice_pub, alice_priv = gen_secret(G)
    blake_pub, blake_priv = gen_secret(G)

    shared = alice_pub * blake_priv
    ct = encrypt(shared, flag)

    assert shared == blake_pub * alice_priv
    assert decrypt(shared, ct) == flag

    print("alice_pub =", alice_pub)
    print("blake_pub =", blake_pub)
    print("ct =", ct)

Challenge Files

Solution

As with this kind of problem, the idea is to map the given group to a group where DLP can be easily solved. We can verify via Brahmagupta's identity that point addition does result in another point on the ellipse. We are also given a generator $g = (g_x,g_y)$ and the challenge works in the group generated by $g$. We shall call this group $E$. This inspires the mapping $\phi: E \rightarrow F_p[u] / (u^2+a)$ defined as $\phi(x,y) = x + uy$. A quick verification shows that $(x,y) + (z,w) = \phi(x,y) \phi(z,w)$. The image of $\phi$ is hence a subgroup of the multiplicative group of $F_p[u] / (u^2+a)$, specifically the group generated by $g_\phi = \phi(g) = g_x + ug_y$. Hence every element of $E$ can be expressed as $g_\phi^n, \; n \in \mathbb{Z}$ for some $n$.

The order of $E$ is equal to the order of $g_\phi$ in $F_p[u] / (u^2+a)$. We hence show that $g_\phi^{p+1} = 1$:

\[\begin{aligned} g_\phi^{p+1} &= (g_x + u g_y)^{p+1} \\ &= g_x^{p+1} + g_x^p g_y u + g_xg_y^p u^p + g_y^{p+1} u^{p+1} & \text{Freshman's dream uwu}\\ &= g_x^2 + u^{p+1} g_y^2 + u (1 + u^{p-1}) g_x g_y \\ &= g_x^2 + a g_y^2 & a \text{ is a quadratic residue} \\ &= 1 & g \text{ is on the curve} \end{aligned}\]

Since the order of $E$ is $p+1 = 2^{521}$, the order is extremely smooth. I specifically chose the value of $p$ and $a$ for this to be the case. DLP can hence be solved in $E$ via Pohlig Hellman. Recovering the flag is as follows:

import sys
sys.path.append("../distrib")

from ecc import *
from out import *

ax,ay = alice_pub
blake_pub = Point(curve, *blake_pub)

_.<x> = PolynomialRing(ZZ)
R.<isqrta> = GF(p).extension(x*x + a)
alice_priv = discrete_log(ax + isqrta*ay, gx + isqrta*gy)
shared =  blake_pub * int(alice_priv)

print("Flag:", decrypt(shared, ct).decode())

DLP

Category: Crypto
Intended Difficulty: Hard
Solved: 19
Points: 884
Flag: SEE{ca66f51d61e23518c23994777ab1ad2f1c7c4be09ed3d56b91108cf0666d49d1}

Huh wait, but I thought DLP is hard.

The challenge provides $n$, $g$ and $g_m$.

$n$ is made up of large primes and we are given the prime factorisation
$g\equiv g'^{\prod_i p_i-1} \mod n$, where $g'$ is an element in $\mathbb{Z}/n\mathbb{Z}^\times$ guaranteed to have an order that's a divisor of $n$ (order isn't divisible by some small prime). This means $g$ has order a divisor $A = \prod_i p_i^{w_i-1}$.
$g_m \equiv g^m \mod n$ where $m$ is a random integer smaller than $A$.

We are to recover $m$.

Challenge Files

So apparently this challenge is an overlap with a challenge from m0lecon >-<. When I wrote this challenge I wasn't thinking of $p$-adic numbers, though that is a cool way to look at it.

Solution

Consider a simpler problem $A$: Given $g \equiv g'^{p-1} \mod n$ and $g_m \equiv g^m \mod n$, with $n = p^w$, $p$ be a large prime, $g'$ a generator and $1 < m < p^{w-1}$. Find $m$.

Lemma 1:

Given $g = g'^{\phi(p^k)} = g'^{(p-1)p^{k-1}}$ and $g_m = g^m$, where $k < w$ and $g'$ a generator of $\mathbb{Z}/p^w\mathbb{Z}^\times$. Then,

\[\begin{aligned} a &= (g - 1)/{p^k} \\ b &= (g_m - 1)/{p^k} \\ m &= b a^{-1} \mod \; p^k \end{aligned}\]

We shall refer to this operation as $m = \text{DLPGP}(g, g_m, p, k)$.

Proof:

We shall work in $\mathbb{Z}/p^{w'}\mathbb{Z}^\times, \; w' = \min(w, 2k)$

$g^m \equiv 1 + r_mp^k \mod p^{w'}$ where $0 \le r_m < p^k$ due to euler's theorem. Furthermore, $g^{m_1}g^{m_2} \equiv 1 + (r_{m_1} + r_{m_2})p^k \mod p^{w'}$. The map $\mu: m \rightarrow r_m$ is hence an isomorphism from the subgroup generated by $g$ and the subgroup of $\mathbb{Z}/p^k\mathbb{Z}$ generated by $r_1$. We define $\mu = \mu_0 \mu_1$ where $\mu_0: m \rightarrow g^m$ and $\mu_1(g) = (g-1)/p^k$. We have $m = \mu_1(g^m)\mu_1(g)^{-1}$.

Back to problem $A$, we have $m = m_0 + pm_1, \; m_0 = \text{DLPGP}(g, g_m, p, 1)$, and so we'd have to find $m_1$ given $g^{pm_1} = g_m g^{-m_0}$. Notice that $m_1 = (\text{DLPGP}(g^p, g^{pm_1}, p, 2) \mod p) + p m_2$? We can recursively find the value of $m_i$ until $k = w$, where we would have finally recovered $m$. (Note: I took DLPGP(...) mod p for ease of implementation).

I refer to the operation of solving problem $A$ as $m = \text{DLP}(g, g_m, p, w)$.

Now consider the original problem in the field $\mathbb{Z}/n\mathbb{Z}^\times$ that's not a prime power. Reducing into $\mathbb{Z}/p_i^{w_i}\mathbb{Z}^\times$ we have, $g_m \equiv g'^{m (p_i - 1) \prod_{j!=i} {p_j - 1}} \equiv g_i^{m (p_i - 1)}\mod p_i^{w_i}$, $g_i = g'^{\prod_{j!=i} {p_j - 1}}$. We hence have $m \equiv \text{DLP}(g_i^{p_i - 1} \equiv g \mod p_i^{w_i}, g_m \mod p_i^{w_i}, p_i, w_i) \mod p_i^{w_i - 1}$. We can hence find $m \mod p_i^{w_i - 1}$ for all $(p_i, w_i)$ and perform CRT to get $m$!

from params import g, gm, n
from functools import reduce
from hashlib import sha256

def product(l):
    return reduce(lambda a, b: a*b, l)


def dlp_gp(g, gm, p, k):

    """
    Returns m%p^k given gm = g^m = (g'^(p-1)) ^p^(k-1)*m mod p^k
    """

    gr = int(g - 1) // p**k
    gmr = int(gm - 1) // p**k
    return int((gmr * pow(gr,-1,p**k)) % p**k)


def dlp(g, gm, p, w, _d=1):
    
    """
    Returns m%p^(w-1) given gm = g^m = (g'^(p-1)) ^ m mod n
    """
    
    if _d == w: return 0
    
    # m = m1 + p^k*m', g^pm' = gpm
    m1 = dlp_gp(g, gm, p, _d) % p
    gpm = gm * Zmod(p**w)(g)**(-m1)
    gp = pow(g, p, p**w)
    
    return m1 + p*dlp(gp, gpm, p, w, _d+1)


primes, power = n
n = product(p**w for p,w in zip(primes, power))
m = [[dlp(g%p**w, gm%p**w, p, w), p**(w-1)] for p,w in zip(primes, power)]
m = int(CRT_list([x for x,_ in m], [y for _,y in m]))

print(sha256(m.to_bytes((m.bit_length()+7)//8, "little")).hexdigest())

RC4

Category: Crypto
Intended Difficulty: Easy (oops)
Solved: 9
Points: 977
Flag: SEE{Lo0K_rc4_w4s_Writt3n_wh3n_n0body_kn3w_sh1t}

1994 crypto go brrr

The challenge implements a modified RC4 that does not loop over the key during the key scheduling. The flag is also encrypted 0x100000 times with different keys of length 192, consisting of the characters 1234567890abcdef and we are given the ciphertext.

See here for the RC4 implementation:

import os

def rc4(key:bytes, pt:bytes) -> bytes:
    
    s = [*range(0x100)]
    j = 0
    for i in range(len(key)):
        j = (j + s[i] + key[i]) & 0xff
        s[i], s[j] = s[j], s[i]
    
    i = 0
    j = 0
    ret = []
    for c in pt:
        i = (i + 1) & 0xff
        j = (j + s[i]) & 0xff
        s[i], s[j] = s[j], s[i]
        k = s[(s[i] + s[j]) & 0xff]
        ret.append(k^c)

    return bytes(ret)

def gen_rand_key():
    return os.urandom(96).hex().encode()

if __name__ == "__main__":

    from secret import secret
    pos_flag = b"abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890_"
    assert all(f in pos_flag for f in secret)
    
    ct = b"".join(rc4(gen_rand_key(), secret) for _ in range(0x100000))
    open("ct", "wb").write(ct)
    print("Flag: SEE[%s]"%secret.decode())

Challenge Files

I actually intended for this challenge to be the easiest of all my crypto challenges, but it ended up being the least solved, which was a surprise.

Solution

So the intended solution was to look up RC4 and see that RC4 has a problem with bias in the byte stream. Given that we're cutting short the key scheduling and using keys within a very restricted character range, we should expect the bias to be a lot worse.

Here's the bias of the first 10 bytes of the byte stream, from 0x100000 samples:

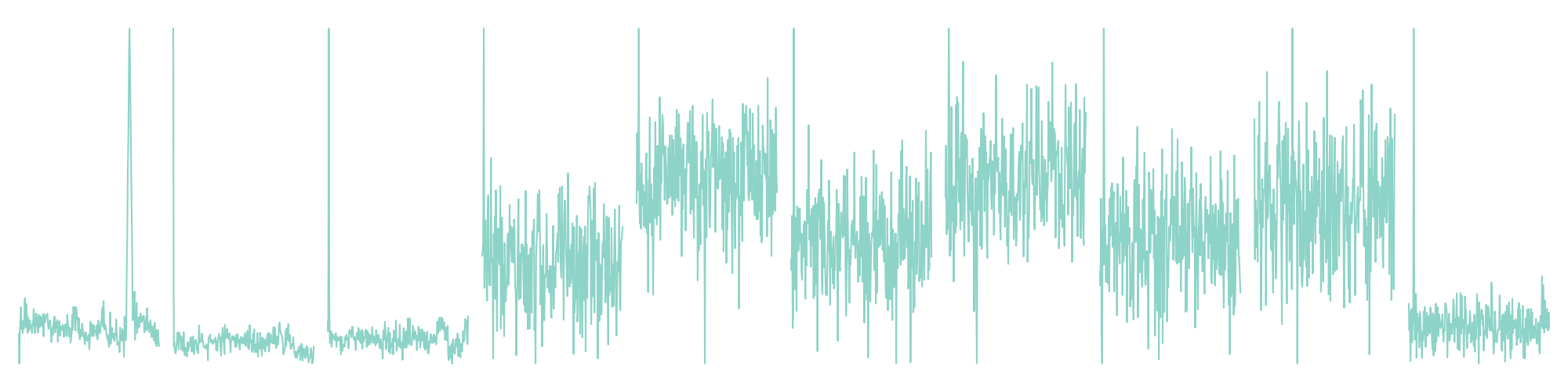
RC4 bias

To recover the nth byte of the flag, we just have to take the most common character in the in the byte stream at that index, and xor it with the most common character in the ciphertext at that index.

# pypy go brrrr
# pypy solve.py

import sys
sys.path.append("../distrib")

from collections import Counter
from rc4 import *

ct = open("../distrib/ct", "rb").read()
flag_len = len(ct)//0x100000
ct = [ct[i*flag_len:(i+1)*flag_len] for i in range(len(ct)//flag_len)]

samples = [rc4(gen_rand_key(), b"\0"*flag_len) for _ in range(0x1000000)]
pos_flag = b"abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890_"

flag = []
for idx in range(flag_len):
    
    c = Counter([i[idx] for i in samples])
    y = [c[i] if i in c else 0 for i in range(0x100)]
    k = y.index(max(y))

    c = Counter([i[idx]^k for i in ct])
    p = [(c[f], chr(f)) for f in pos_flag]
    p = [y for _,y in sorted(p, key=lambda x:-x[0])]

    # Print top 4 candidates
    print(" ".join(p[:4]), idx)
    flag.append(p[0])

# One or two chars might be wrong, but can be guessed
#
#            .---(should be 4)
#     _______v__________________________________
# SEE{Lo0K_rcf_w4s_Writt3n_wh3n_n0body_kn3w_sh1t}
print("SEE{" + ''.join(flag) + "}")

It's Right There

Category: Reversing
Intended Difficulty: Hard
Solved: 1
Points: 1000
Flag: SEE{GPU_0nLy_RaytrAC3r_p1x3l}

Couldn't you just like, idk, move a little to the right?

The players are given a binary Its-Right-There.exe as well as the DLLs d3d9.dll and D3DX9_43.dll, which are (were as of windows 11) packaged with windows DirectX 9 whatever. Running the binary produces a small window that shows a scene with the flag visible. Unfortunately for the player, the flag extends out beyond the camera into the void:

Challenge Files

Hints Given:

24th hr mark:

The relevant code isn't executed on the cpu

36th hr mark:

Metadata

So, the team r3kapig (the team in 1st place) managed to solve this challenge in the last 20 minutes of the competition, which, wow bravo. I'm happy that a team managed to solve this and also enjoyed the challenge *^-^. Also, a moment of silence for these teams who were so close:

Solution

The binary is written to be similar in style to a regular demoscene binary, except that the shaders are precompiled. As such, the binary is packed with Crinkler. Furthermore, the entire scene is rendered on a pixel shader, with the raytracing logic, lighting, materials and scene geometry all defined within the pixel shader.

Bypassing Crinkler is trivial. The binary unpacks in memory and can be analysed by simply stepping past the unpacking code. By reversing the d3d9 and d3dx apis used would show that there are two shaders:

Pass through vertex shader (vertex shader that literally does nothing)
A Very Big pixel shader

The pixel and vertex shaders are terminated by 0000ffff and can be dumped out to be analysed. By inspecting the strings it can be shown that the pixel shader uses ps_3_0 language model, which has some reversing tooling on github.

Author's Note:

ps_3_0 is chosen because:

~~Has a decent disassembler~~

Buggy af

Later models up till ps_6_0 has absolutely no tooling to my knowledge bcuz microsoft doesn't wanna release them and nobody bothered to write them.

Allows bytecode patching (later shader models have annoying checksums)

~~Microsoft an assembler for it within d3dx.dll. (Later shader models up until 6.0 don't have an assembler).~~

Doesn't matter since disassembler's buggy af

It's between ps_3_0 and ps_6_0 and I'm more familiar with ps_3_0.

Now, you can attempt to disasemble the pixel shader, but all the disassemblers I've found on github are wrong. Attempting to reassemble with D3DXAssembleShaderFromFile will just yield a ton of errors. I actually tried to fork the project and fix the disassembly but it really wasn't worth the effort.

However, the parsing of the constants used in the shader is trivial. I just patched the disassembler to give me the byte offsets to all these constants. These constants control various attributes of the scene, such as the render distance and colour. The idea is that the player can bytepatch these constants to display the full flag.

I wrote to run the binary and bytepatch the pixel shader in memory with gdb. With this setup, the player can then modify the constants and run the script try.py to see the changes.

Click here to see the script:

import struct
import os

# Partially parsed orig_ps30.bin to get the constants
config = {
    396: ('c5', 
        ('0.578267335892', '0.0722834169865', '7.99900007248', '0.125')),
    420: ('c6', 
        ('-8.0', '-9.0', '-10.0', '-11.0')),
    444: ('c7', 
        ('-12.0', '-13.0', '-14.0', '-15.0')),
    468: ('c8', 
        ('-16.0', '-17.0', '-18.0', '-19.0')),
    492: ('c9', 
        ('-20.0', '-21.0', '-22.0', '-23.0')),
    516: ('c10',
         ('0.0', '1.0', '0.0010000000475', '-0.800999999046')),
    540: ('c11',
         ('81.2772903442', '0.0', '0.899999976158', '-0.34999999404')),  
    564: ('c12',
         ('6.28318548203', '-3.14159274101', '0.0', '-0.0299999993294')),
    588: ('c13',
         ('-4.0', '-5.0', '-6.0', '-7.0')),
    612: ('c14',
         ('-24.0', '-25.0', '-26.0', '-27.0')),
    636: ('c15',
         ('0.5', '50.0', '2.0', '0.159154936671')), # Modified c15.y, 5->50
    660: ('c16',
         ('-0.0', '-1.0', '-2.0', '-3.0')),
    684: ('c17',
         ('0.5', '0.40000000596', '-0.800000011921', '1.10000002384')),  
    708: ('c18',
        ('-67.442855835', '12.1051282883', '-0.600000023842', '-0.550000011921')),  
    732: ('c19', 
        ('0.125', '0.875', '0.5', '-0.0500000007451')),
    756: ('c20',
        ('1.25', '-0.10000000149', '-0.0010000000475', '-0.101000003517')),
    780: ('c21', 
        ('-0.5', '-1.04716670513', '1.04716670513', '-20.0')), # Modified c21.w, -3.0 -> -20
    804: ('c22',
        ('0.00999999977648', '0.0500000007451', '0.070000000298', '0.0')),
    828: ('c23',
        ('0.199999988079', '-0.699999988079', '0.300000011921', '0.333333343267')), 
    852: ('c24', 
        ('4.0', '0.40000000596', '1.20000004768', '0.00999999977648')), 
    876: ('c25', 
        ('0.179999992251', '0.216000005603', '0.324000000954', '0.0')), 
    900: ('c26', 
        ('0.899999976158', '1.08000004292', '1.62000000477', '0.0')),   
    924: ('c27',
        ('0.318309903145', '2.60000014305', '3.40000009537', '1.59154939651')),     
    948: ('c28',
        ('11.4000005722', '9.4000005722', '0.0159154944122', '-0.070000000298')),   
    972: ('c29', 
        ('0.5', '0.40000000596', '-0.800000011921', '1.09899997711')),  
    996: ('c30',
        ('0.500999987125', '-0.799000024796', '100', '0.499000012875')), # Modified c30.z 1.10000002384 -> 100
    1020: ('c31',
        ('0.400999993086', '1.10100007057', '0.398999989033', '0.00300000002608')),
    1044: ('c32', 
        ('0.629999995232', '0.756000041962', '1.13399994373', '2.5')),
    1068: ('c33', 
        ('4.5', '5.40000009537', '8.10000038147', '0.0')),
    1092: ('c34', 
        ('0.0', '-0.0010000000475', '-2.0', '0.0')), # Modified c34.w 3 -> 0
    1116: ('c35', 
        ('0.20000000298', '0.800000011921', '0.0', '0.0')),
    1140: ('c36', 
        ('-1.0', '0.0', '1.0', '0.019999999553')),
    1164: ('c37',
        ('-20.7516479492', '8.64651966095', '-15.5637359619', '38.0446891785')),
    1188: ('c38',
        ('-57.0670318604', '103.758239746', '-84.7358932495', '-17.2930393219')),
    1212: ('c39',
        ('-29.3981685638', '65.7135543823', '-44.9619026184', '95.1117172241')),
    1236: ('c40', 
        ('-77.8186798096', '0.0', '70.9014663696', '13.8344316483')),
    1260: ('c41',
        ('-3.45860791206', '-34.5860786438', '6.91721582413', '-10.3758239746')),
    1284: ('c42',
        ('0.5', '0.500999987125', '0.40000000596', '0.499000012875')),
    1308: ('i0', 
        ('200', '0', '0', '0')),
    1332: ('i1', 
        ('28', '0', '0', '0'))
}

def apply_config(config):

    return "\n".join([
        'set {char [16]} %s = ' % hex(0x421FD0 + o) + \
        ",".join(
            r"0x"+format(i, "02x") for i in (
                struct.pack("<ffff", *map(float, v)) if r[0] == "c" else
                struct.pack("<iiii", *map(int, v))
            )
        )
        for o, (r, v) in config.items()
    ])

def write_config(str):
    open("gdb_input", "w").write(str)

def run():
    os.system("(type gdb_input && cat) | gdb Its-Right-There.exe")

write_config("\n".join([
    "b *0x004000D3", # Just before unpack
    "r", # Unpack!

    "b *0x00420314", # push address of pixel shader to stack
    "c", # Run!

    apply_config(config),

    "c", # Run!
    ""
]))

run()

Playing around with the constants yields the following interesting ones:

def c15, 
    0.5, 
    5, // <-- Render distance
    2, 
    0.159154937

def c21, 
    -0.5, // <-- Controls camera
    -1.04716671,
    1.04716671,
    -3 // <-- Controls camera

def c30, 
    0.500999987, 
    -0.799000025, 
    1.10000002, // <-- Floor height
    0.499000013

def c34, 
    0, 
    -0.00100000005, 
    -2, 
    3   // <-- Controls visibility

There is also the following constant c17.x that at first glance controls the x-position of the flag. Changing it will shift the flag into view. However, the compiler has reused c17.x to also control the distance between the characters, causing the flag to get fucked up when its value changes too much.

By modifying the following constants:

c15.y: 5 -> 50: Render distance increase to 50
c21.w: -3 -> -20: Move the camera wayyy back
c30.z: 1.10000002 -> 100: Move the floor so far down it disappears from view
c34.w: 3 -> 0: Maximum visibility (everything becomes white)

the player moves the camera in such a way that the full flag is visible:

How it's made

So! Most of the work actually went into writing the 500 line pixel shader so that's all I'm going to talk about. You can view the source here: pixel.hlsl.

Author's Note: This challenge is cursed okay, it blue-screened my poor laptop many times, and did so twice just from writing this writeup. I also had to fight the compiler because compiling such a huge pixel shader isn't exactly a common use case.

Scene representation

The scene is represented with Distance Functions which I copied from the legend Inigo Quilez. The lighting and shadows and materials are essentially hand-painted to look good in this scene, and bleed and subscattering and stuff are just approximated (See LightPoint_computeBleed).

Drawing the flag

The characters of the flag are also represented as distance functions. However, instead of computed analytically, the distance is sampled from a texture:

In fact, this texture is the biggest contributing factor for the final size of the executable (13kb). The size of this texture alone is 7kb.

The distance function of the flag is computed as such:

float c = _lS;
int j = 0;
for (int i = 0; i < 28; ++i) {
    float _d = Primitive_sdChar3D(p, .03, c);
    c += flag[j]; j += 1;
    d = min(_d, d);
    p.x += .5;
}
float _d = Primitive_sdChar3D(p, .03, c);
d = min(_d, d);

to prevent recovering the n-th character of the flag by simply bytepatching the constant n to be 0 or smth. In addition, the index of the character in the texture is multiplied by the constant CONFUSE=1.729304 so that the constants that corresponds to the character indices aren't as obvious.

To Infinity

Category: Misc
Intended Difficulty: Hard
Solved: 6
Points: 991
Flag: SEE{Sayonara-Wild-Heart_91629432713d02f}

To infinity and beyond

Players are given a game where they are placed into room n=31415..., and can move up, down, left or right. Moving up increments the room number, down decrements the room number, and going left or right moves the player to room 1/n mod 2^255-19 (The modulus is a prime btw!). This has the nice effect that going the opposite of where you came from brings you back to the same room *^-^.

Players are tasked to reach room $\infty$ in less than 1000 moves, where presumably they'll get the flag. This involves reaching room 0 and doing a inverse. There's also a leaderboard that ranks players on the least number of moves to reach $\infty$.

So this challenge is really more of a collaborative effort between me, @Neobeo and @Zeyu2001. Neobeo came up with the original challenge idea, I speedran the implementation in about 6 hours (and it shows), and Zeyu is left to deal with setting up the infra needed to have multiple instances share the same leaderboard. We had hoped to see some friendly competition on the leaderboard but it's alright. Also since most players probably didn't actually see room $\infty$ since they would have bypassed the ui, here's what the room looks like:

If you've come to this post via the homepage you'll probably recognise the heart. I was too lazy to define a new geometry to use.

Hints Given:

24th hr mark:

Continued fractions might come in handy here.

Solution

In the end I think the shortest solution achieved by players was by @4yn, with a score of 659? Me and Neobeo a 367 solution, but we submitted an 888 solution to the leaderboard to encourage players to beat. Neobeo also showed that there's a lower bound of 316 so our solution was close to optimal (if not optimal) but that's for Neobeo to write about. I'll link to his writeup here if he ends up writing it, he proved several more cool results.

From now I'll be representing the solutions as a string of -, + and /, representing increment, decrement and invert.

367 Solution:
---/--/-/-/--/--------/--/--/--/---/--/----/
-/----/--/----/-/---/--/--/-/-/-/-/--/-/--/-
-/--/---------/-/----/-/--/-----/------/----
-/--/-/-/-/----/-/-/--------/----/--/--/-/-/
------/-/-/-/---/---/-/--/-/---/-/-/--/-/--/
----/-/-/-/----/----/-/---/-/--/--/--/------
/--/---/----/-/----/-/-/-/-/-/---/-/-/-/-/--
/--/-/-/---/-/--/--/--/---/-/-------/---/-/-
/-/-/---/-----/

I'll briefly go through how we reached the 367 solution. Say we start at room n and p is the modulus. We need a way to measure how close we are to 0. If you're currently in room m, a good measure is how large can the smallest integers a and b be such that a/b mod p = m. Continued fraction expansion should come to mind. One can verify that the continued fraction expansion of say n/(p+1) would result in a valid solution to 0. E.g. if we started at n=5, p=7, we get the expansion [0; 1, 1, 1, 2], corresponding to the solution /-/-/-/--.

More generally, we can consider the expansion of (a*p + n)/(b*p + 1) for integers a and b. I had the insight to perform LLL on every room m we visit, to find small integers x/y = m mod p and continue expansion from there. Bruteforcing a and b, we get a solution of roughly 390+.

Neobeo then realised that you only have to perform LLL on the first room, since on subsequent rooms the LLL wouldn't change the fraction expansion (most of the time). This allowed him to bruteforce billions of possible a and b, and results in multiple 367 solutions (the above is just one of them). Neobeo also wrote an extremely succinct script that does whatever I've just described:

# The one-liner that generates the `367` solution
''.join('-'*x+'/'for x in(lambda r:r[1]/r[0])(vector([8639,166])*matrix([[1,start],[0,p]]).LLL()).continued_fraction())

Playtested Challenges

So I also playtested some challenges in SEETF. I won't write too much about this, but I'd like to share unique solutions that I found to challenges I attempted. Might update this section if I feel like it isn't too much of an overlap with other writeups.

Neutrality

Category: Crypto
Intended Difficulty: Hard
Solved: 5
Points: 995
Flag: SEE{50-50_can_be_leaky_4c17bf2a20c4a8df}
Author: Neobeo

Author's Writeup

In this challenge we are given a flag xored with a random bitstream 200 times. For each bitstream, exactly half of the bits are 1s (hence the name Neutrality).

from secrets import randbits
from Crypto.Util.number import bytes_to_long

# get a one-time-pad in which exactly half the bits are set
def get_xorpad(bitlength):
    xorpad = randbits(bitlength)
    return xorpad if bin(xorpad).count('1') == bitlength // 2 else get_xorpad(bitlength)

def leak_encrypted_flag():
    from secret import flag
    return bytes_to_long(flag.encode()) ^ get_xorpad(len(flag) * 8)

# I managed to leak the encrypted flag a few times
if __name__ == '__main__':
    for _ in range(200):
        print(leak_encrypted_flag())

My Solution

If you were to try using Z3 to solve, you'll find that it runs really slow. The issue is that this condition: exactly half the bits are set is really hard to model as a SAT problem. So the question arises: Is there another way to model this problem that's significantly more efficient?

So I was thinking, Integer Programming would model the neutrality condition real efficiently, but how do you model XOR efficiently? In other words, say x, y and z satisfies x^y = z. How do we define linear constraints on x,y,z such that it satisfies our XOR constraint?

The idea is to consider the convex hull of the points (x,y,z) where x^y = z. Each face of the convex hull would yield a linear constraint, for a total of 4 linear constraints (for each of the face of the simplex). In fact, this method can model any boolean function, though it blows up as you add more variables. For the case of XOR, our convex hull is:

x + y - z >= 0
x - y + z >= 0
x - y - z <= 0
x + y + z <= 2

Now we model the whole problem with Integer Programming, taking into account the flag format:

from Crypto.Util.number import bytes_to_long, long_to_bytes
from mip import Model, xsum, BINARY
import time
t = time.time()

flen = 320
ct = [*map(int, open("distrib/output.txt").read().split("\n")[:-1])]
ct = [[*map(int, format(c, "0320b"))] for c in ct]
nct = len(ct)

model = Model()

flag = [*map(int, format(bytes_to_long(b"SEE{" + b"\x7f"*(40-5) + b"}"), "0320b"))]
for i in range(32, 320-8):
    if flag[i]: flag[i] = model.add_var(var_type=BINARY)

keys = [
    [model.add_var(var_type=BINARY) for i in range(flen)]
    for j in range(nct)
]

for k in keys:
    # Models 'neutrality'
    model += (xsum(k) - flen//2) == 0
    
for c,k in zip(ct, keys):
    for x,y,f in zip(c,k,flag):
        # Models x^y = f
        model += (+x+y-f) >= 0
        model += (+x-y+f) >= 0
        model += (-x+y+f) >= 0
        model += (-x-y-f+2) >= 0
        
model.optimize()
flag = long_to_bytes(int("".join([str(int(f if type(f)==int else f.x)) for f in flag]), 2))
print("Flag:", flag.decode())
print("Time:", time.time() - t)

# Flag: SEE{50-50_can_be_leaky_4c17bf2a20c4a8df}
# Time: 95.57503890991211

This solves in about 1.5 min *^-^.

Notable Creative Solution: @Javalim actually managed to solve the problem by modelling it as a differential problem and optimizing it with Pytorch.

More on this site:

SEETF 2022 Author Writeup

Metadata

The True ECC

Solution

DLP

Solution

RC4

Solution

It's Right There

Hints Given:

Metadata

Solution

Other solutions

How it's made

Scene representation

Drawing the flag

To Infinity

Hints Given:

Solution

Playtested Challenges

Neutrality

My Solution