Greyhats 2022 Finals Writeup
Writeups for challenges I found interesting
Metadata
I participated in Greyhats CTF by NUS Greyhats with @Zeyu2001 and @Rainbowpigeon and we got 4th place in both the Quals and Finals. The Finals was the first physical CTF but I spent the first 80% alone (having a meeting room to myself ^-^) since Zeyu was on a plane and Rainbowpigeon would rather work at home. Kinda my first time meeting all the people I only know via their discord handle.
It was overall a pretty fun CTF (and the first one I lost sleep over), but I can't help feeling salty that I was so close to solving two more challenges.
I'll only be writing up challenges I found interesting (biased towards Crypto). Also I procrastinated way too long in doing the writeup, the server's down and so I can't get the challenge info. But I'm writing this anyway as sort of a record.
Oneliner
- Category: Rev
- Flag:
grey{quite_big_no}
We are given a huge python file that's nearly 10mb in size. Most of it consists of one line that checks if a given string is the flag. Here is a snippet:
1
2
3
4
grey = input('i will tell you if you know the flag: ')
assert(len(grey) == 18)
ans = lambda grey: (grey[0] == 'I') if ((grey[1] == 'K') if ((grey[2] == 'j') if ((grey[3] == 'C') if ((gr...
print('good' if ans(grey) else 'bad')
Solution
It took… one full minute to open the file on my potato laptop in notepad++. I then decided that I'll try my best to never open the file.
The intended solution involved finding patterns in the file. I didn't do that but instead opted for transpiling the huge expression ans into a Z3 expression and solving for it.
The good thing is that ans is basically a huge ternary ? if ? else ? with some predicates like 0x3cab ^ 0x823a - 0x6235 == 0x1dbb. This means that my transpiler can be relatively small since there's so few cases to consider. I opted for using the ast module to convert the expression into a my own AST.
Since the expression is so simple, my own “AST” is simply a nested tuple. I recursively traverse (depth first search) the ans expression to build the tuple:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import ast
def parse_compare(compare):
if isinstance(compare.left, ast.Subscript):
idx = compare.left.slice.value.value
val = ord(compare.comparators[0].value)
assert isinstance(idx, int)
assert isinstance(val, int)
return idx, val
if isinstance(compare.left, ast.BinOp):
return eval(compile(ast.Expression(body=compare), filename="", mode="eval"))
if isinstance(compare.left, ast.Constant):
return eval(compile(ast.Expression(body=compare), filename="", mode="eval"))
raise Exception()
def parse_ifexp(ifexp):
# body if test else orelse
return parse(ifexp.test), parse(ifexp.body), parse(ifexp.orelse)
def parse(expr):
if isinstance(expr, ast.IfExp):
return parse_ifexp(expr)
if isinstance(expr, ast.Compare):
return parse_compare(expr)
if isinstance(expr, ast.Constant):
return expr.value
raise Exception()
code = open(r"oneliner.py").read()
tree = ast.parse(code)
root = tree.body[0].value.body
p = parse(root) # p is my ast!
I briefly considered manually writing the path exploration before deciding to simply transpile to Z3, and asking Z3 to solve the expression.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from z3 import *
def traverse(p):
if not isinstance(p, tuple):
if not isinstance(p, bool):
err[0] = p
raise Exception()
return p
# Constraint
if len(p) == 2:
idx,val = p
return flag[idx] == val
if len(p) == 3:
# body if test else orelse
body, test, orelse = p
return If(
traverse(test),
traverse(body),
traverse(orelse)
)
flag = [BitVec("f%d"%i, 8) for i in range(18)]
con = traverse(p) == True
s.check()
m = s.model()
print(bytes([m[c].as_long() for c in flag]).encode())
# > b'giFGvOiGIHkMIjEDF?'
Wait weird… giFGvOiGIHkMIjEDF? isn't the flag? Running it through oneliner.py returns good so why isn't this the flag?
Turns out you also need to enforce the flag format, and then there's a unique solution for the flag:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
s = Solver()
s.add(con)
s.add(flag[0] == ord("g"))
s.add(flag[1] == ord("r"))
s.add(flag[2] == ord("e"))
s.add(flag[3] == ord("y"))
s.add(flag[4] == ord("{"))
s.add(flag[-1] == ord("}"))
s.check()
m = s.model()
print(bytes([m[c].as_long() for c in flag]).encode())
# > b'grey{quite_big_ah}'
Polynomial
- Category: Crypto
- Flag:
grey{58693e0cdfc89ac44579cfd6343ee2854afba49c}
We are given a typical Discrete Logarithm Problem (DLP) setup. We work in the ring $R = \mathbb{F_p}[x]/m(x)$, where $m(x)$ is a degree 14 polynomial. We are also given a generator $g \in R$, , and for some random $a,b < 2^{510}$, we are given $A = g^a$ and $B = g^b$. We are to compute $S = g^{ab}$, which implies solving the DLP on $R$.
See challenge source:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from secrets import randbits
from hashlib import sha512
p = 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314719
F.<x> = GF(p)[]
a = randbits(510)
b = randbits(510)
g = 10384700499901535223919857506931232553401454394050379769765536307411968493838004422860649467991480530544778693163785053677427830431506192830777188178741979*x^13 + 10775520212786796763090742106063246877023962231910846111765121211871361736681070722062710288430645172043594507172708588801886370620034129529660295091344714*x^12 + 10521435056168881308802457152558268247224996509743289893456461536355164124036962673429912989790359529422726713260072965981394775587018074701100959277041438*x^11 + 2910769218278645393074704153789332602198429517001051568963424607574892873574455078910571015774546826251842852202984306770698501326239463290815739513801408*x^10 + 6036470331023831078469115007165589411535635349568587449591953353255982788047373691902296849864056809898972961092665748439651880217260182985599401868227768*x^9 + 591363200400932000253212680640847460621278725044891665431126301925549139313954453668319310368430374470695814023600916221362057535092477565146095828664143*x^8 + 339728148077126742885012314649290541366019041740296720917964996484980130672990268208853763469829278831103124996711026038960532520865749721591051491618046*x^7 + 9345178860497811526494439131161805811589252168050371259704533574037091061384155798044835345451752128106493409522585805664993526018802170168776561737177405*x^6 + 2433961457253371737132916031569862717283506136190359751978675228599240290238760020108980892787353290833475072080707646130935623875903542976991420612709108*x^5 + 8527594305290216865886606166815555754056982082861349112757967072841919060996898573828062378313042182966638346857209511236313154318514685181533840959436675*x^4 + 5358454129102757417173047896189904677914411242798565121290776098710525483492218802190588093736382975167501683663705988501938074105638487388662840237729835*x^3 + 7817596260676713181647087350155902793146961592182806824490469880694903167872794700457751972446624803488056186714736669838580426781164909724443552865808422*x^2 + 10002477743570459253843620504391443026917382176854435882506194792206061761603041265500473493242349055688165822800467197000288376363652222128838500806592826*x + 3313769437884440593833448168905257650699214782951924810218492479285877956513092588118164942972388916129919644948861769119998094634206681093262295531975717
mod = x^14 + 2*x^13 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314696*x^12 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314681*x^11 + 186*x^10 + 252*x^9 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314106*x^8 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311313975*x^7 + 806*x^6 + 886*x^5 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314397*x^4 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314523*x^3 + 109*x^2 + 11421263358678931360891521159249804547289144488527637700007933797479949987203617883047002297051855220559889265348542601551941960420936888353172939311314701*x + 1
def power(a, b, mod):
res = 1
while b > 0:
if b & 1:
res = res * a % mod
b >>= 1
a = a * a % mod
return res
def getFlag(x):
key = ",".join(map(str, list(x))).encode()
return 'grey{' + sha512(key).hexdigest()[:40] + '}'
A = power(g, a, mod)
B = power(g, b, mod)
S = power(A, b, mod)
FLAG = getFlag(S)
print(A)
print(B)
print(FLAG)
# A = 4847270505274230484459549005292280567571584711681937343494273320685581759701293615921302055362985969549394710114999960717567820282719257283814267855545515*x^13 + 10219401030167960074046819572611210551008527492516803819958372605553648863392645743965592550524032854129434341214727645596813796020166571894571079320811357*x^12 + 7437101399711554526467993921186467021973517069177876899089534926333306096388239434690538142585662600072281814685191569847839006857370666384270985401699674*x^11 + 6531644882142403272525867050212429645096347534608561543591926527658273154845416847860082693055696195456535683021149054618600918902360030518388766308604345*x^10 + 917624731101506575101029182559524973371598092733839958974617254459022834195474768527726713006874083684646003679628915394928839792291893053238770042380982*x^9 + 10134221694817861757881123697189330223757964230942432120084596742854774177059354146372824523352940268311177164657224547938032605431319529535095841249615840*x^8 + 8497050176302501208853838786508739444883767700203354716798374700594047427708347707092200898152538208810508443617380051403347368464032113721277238229509440*x^7 + 3460677029229219935808278507527663872450970471490928484313772261711091276294096956009696492198944886924779167439859071320071125514900702177281192863856875*x^6 + 8530963245334028105504200618844053198887032047474593781748422677392011498369087828107565685897914857008112472141420060568607097949403516995161058606209487*x^5 + 8910798786507050137341263017034267180755842197403028229663275354814519935477897729932244752304893933338109758940262706522632111359468483442558766629387347*x^4 + 5741955362070959989679741521481963593369283371228399361790607741217290797706400087596711590350719011643549882729568302248218047544547024669425243192701832*x^3 + 7579234927949188239058650834515069209385862370736447676512961788005688390117409286970349071509985241949794613592740925877008784526477442653784761452800045*x^2 + 1500479152217397980248563051872357083415999261841186699957798174802766450959318946859973027249243541181675675331367578735735836110280419055318660183259221*x + 10039968702803708137850318426160866360611728484153635779786672231704800169450052028641430432126791846821319282309975298697142867271538843898747268059327192
# B = 6400114883258647786012503823889786895441784961949043817136919974303064746041583644384660783341406668990017545732497313845284777007194693957840706791473549*x^13 + 5681506648461562196271267654189171209582352882494632268453545352889424039792514645037333956100735677767475088873351185969665219795412608963433232897235303*x^12 + 5510647662761624593794785835666583161371149246018228180548333424649800354125555066835832753989248530035467119364262731083819256202094193600751780178204015*x^11 + 327351207606114560271265084688565891866401527363338223735400064189320235871398956888907062613980517107928079209357727174283361242951294038489186922008053*x^10 + 5157383664989876843673594911669788472217727077396548612037190188777586339832725434031008266740300852358016164587492071578230875661467078306340828873894987*x^9 + 6250223931322125407490188422290004821722222322724629159302879641211164705657217238555760156954294312073954006956026825756857619892109929685850156516426711*x^8 + 1392782606912984708893768233216410758546369614122502601949598438133626256484565929701483787732748282044567364231808931004624961772615487278498765896281018*x^7 + 10730687595972697491651138493714645639465917453961375191237725104277988405692246626116202093478721871674655438707175681145977331475462752851006755071879668*x^6 + 6134963578172194182074879699973829102207039261625371234112229688755985692803630779752768516081016504173398436559093818946835058921750123929588196168339316*x^5 + 5938125022941571305741861008315574667399981013852153191357768290006940277748651556017358371706308312561620792957018708386586079895342941435186553082341119*x^4 + 2597526541258324764716691080904414090648576226446139532279612984499980699152100244053803604023295651405632260083413910819678400359673312682295768427800056*x^3 + 6228947521171142328926221282780954970464374792021940320199777734564056333793640363471024730175009431674774833153846393995294860729668594084321570077727438*x^2 + 988384371249784826937163357899115300643301119595369592039018220510285225530411203201347229527854692130285225673137026681487138031530955419220748662396174*x + 7042659972069509520890314908981927240070031817626695809529031744748365560275530478019360663866308648279498997796851164604295514991772243877366447300167741
Solution
It's not immediately obvious but attempting to factor $m(x)$ shows that it's actually a square $m = m'^2$, with $m'$ a polynomial of degree $7$. $R$ is hence not even a domain (since $m'^2 = m = 0$ in $R$).
I considered mapping the problem to $R' = \mathbb{F_p}[x]/(m')$. Since $m'$ is irreducible, $R'$ is a field isomorphic to $\mathbb{F_{p^7}}$. Therefore $R'$ has multiplicative order $p^7-1$. Attempting to factor $p^7-1$ shows that it's not smooth, so the usual Pohlig strategy is out. The solution is probably to map the structure generated by $(g, \times)$ in $R$ to something where DLP is trivial.
I then considered decomposing $g$ into $a m' + b$ (quotient-remainder upon dividing by $m'$). My reason for doing so was to consider the interaction between both components:
\[\begin{aligned} g &= a m' + b \\ g^n &= n a b^{n-1} m' + b^n \mod m'^2\\ \end{aligned}\]I then thought for a long time how I can possibly recover $n$ given $g^n$. Clearly simply considering the modulo $m'$ component isn't enough since that just means solving DLP in $\mathbb{F_{p^7}}$.
At 4.14 AM, having attempted to sleep in the cold comfort of the meeting room table for the past 2 hours, (and giving up and then solving Quantum), I had the epiphany to raise everything to the power $p^7-1$.
Remember how the multiplicative order of $R' = \mathbb{F}_p[x]/(m')$ is $p^7-1$? Taking an element in $R$ to that power absolutely obliterates the modulo $m'$ component. We'll have essentially:
\[\begin{aligned} g^{p^7-1} &= a m' + \textbf{1} \\ {g^{p^7-1}}^n &= n a m' + \textbf{1} \mod m'^2 \\ \end{aligned}\]By taking the quotient of $g^{p^7-1} = q_0 m' + r_0$ and ${g^{p^7-1}}^n = q_1 m' + r_1$ when divided by $m'$, we can compute $n$ simply by taking $q_1 q_0^{-1}$. Since $q_0$ and $q_1$ are associates, we can simply consider $q_1(0) q_0(0)^{-1} \mod p$! We've mapped the problem into computing DLP in the additive group modulo $p$!
Equation 3
- Category: Crypto
- Flag:
grey{Hope_you_like_this_equation_series_:D_k9!LY$jWT&1*%wjPKCo2EnsXB3}
We are to solve a diophantine equation modulo $N$, where $N$ is the product of two large primes $(p,q)$.
Our flag is split into two parts $(p_1, p_2)$ and taken to the power of $d = e^{-1} \mod \phi(N)$ for some known $e$ (just like RSA). Let the result of this exponentiation be $(p_1^d, p_2^d) = (m_1, m_2)$. We are then given the values of $(f,g)$ defined as:
\[\begin{aligned} f &= 13 m_2 ^ 3 + m_1 m_2 + 5 m_1\\ g &= 7 m_2 + 31 m_1 ^ 2 \mod N \end{aligned}\]See challenge source:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import bytes_to_long, getPrime
FLAG = <REDACTED>
n = len(FLAG)
m1 = bytes_to_long(FLAG[:n//2])
m2 = bytes_to_long(FLAG[n//2:])
p = getPrime(1024)
q = getPrime(1024)
N = p * q
phi = (p - 1) * (q - 1)
e = getPrime(2000)
d = pow(e, -1, phi)
m1 = pow(m1, d, N)
m2 = pow(m2, d, N)
f = (13 * m2 ** 3 + m1 * m2 + 5 * m1) % N
g = (7 * m2 + 31 * m1 ** 2) % N
print(f'N = {N}')
print(f'e = {e}')
print(f'f = {f}')
print(f'g = {g}')
# N = 17927320462303249934937883811002903172176765780523264738218843188366231264362958134997396675322722182212946103387542427667614560300824275082930993438796152667358057905501388442666203835655421406331007550762620857458776925047486735156307951871159956726716491719411963027695083171938415102823702868577031391687645311173920337955011217886182822688961228884185499009594127468988403104089260821647176060803872160462815870709958513255136202811139994310113641543989278813854109471924049657836577005690555289636010431314636269606536590316072139220601735271676852874127018524038520010954224014233667071407682730320232372776827
# e = 100577742074524497824622354284958380192395932541541769441112753917086618375934151886811818515255236370430705281962608314561237109077495630714819650375461610661996673790851901731468480295351122714442494101061587758379499719189556551665949945578334563022171989974062582776038308628748868278191588382130551996059296674056234448133968345091765916365446435322213390046139281082768445159669265752911993562659968822979249892785281293997707125331015620097817687624536491945132051369970996889180780899283750458519793860458278758958506958859769783056909579049512924757044155161743553730046009536195889458438629687
# f = 2003951756376962277245326364596092323096230607377054702381631019234315528219853510695662722224615100682500364781873276760728334939695764978309921643283780194990737457777758114510482407391691402452626548736439965238456280273451951586803046081215905097069877827179810815082967302511256271441525836908557322461721657533200100557922535735147226911891969812798091093952987871841259122497133821241295665437561188729345076580897082811617772997121896049516828435778643217903918918265879458528692105196487215822555819641050311803422964795441579496147832806519077135807484008858521044062203786506949496670915303512592707226821
# g = 7842476000748164302616238377802737357115292476364667000564453174629609557251054926850285511197179944483904784694635672100105186390897281910141763726425320305959281506156192418095260350510510648997847344726031269146623789249427231347793868520688988991592777533209678260490936250483388903076779742296927870940127254416263201582230523071473370769350316168840730173343387822957123285098313420379654615838488913383254944175999219974968139986636628467569862338260293900937389611580044080917896692619566739903519816847072924323097877881160608043282469962187110248263940322414184355056247541767071153230286768196602717594692
I didn't solve this during the CTF but was frustratingly close. I got the main inspiration (but didn't realise it) right as I fell asleep at 630am, and only realised the significance after I woke up, 8 minutes before the competition ended. (was trying to solve Disc, which is another challenge I am extremely salty about).
Solution
Let $(F,G)$ be two polynomials in $(m_1, m_2)$ defined as
\[\begin{aligned} F &= 13 m_2 ^ 3 + m_1 m_2 + 5 m_1 - f \\ G &= 7 m_2 + 31 m_1 ^ 2 - g \end{aligned}\]Clearly we are to recover $(p_1, p_2)$, and the main difficulty of this challenge is not knowing the factorisation of $N$. What we are meant to assume (which I was cautious to) is that $p_1$ and $p_2$ are relatively small compared to $N$, which I guess kinda makes sense as $N$ is $2048$ bits.
I spent most of the time screwing around with $N$, or trying to find two polynomials in $m_1$ or $m_2$ with a degree $1$ gcd. But admittedly I didn't spend too much time on this as there were other challenges to be solved (for the first half of the CTF we had essentially two members only).
What I got so far then was that we can find a polynomial of degree $6$ with root $m_1$ by taking $R_{m_1} = \text{Res}_{m_2}(F, G)$, and similarly for $m_2$. If I were to make the above assumption of the size of $(p_1, p_2)$, a plausible approach will be to find a polynomial with root $p_0$ or $p_1$ and use coppersmith to solve.
As you can see in the screenshot above, I had the inspiration to consider the ring $R = (\mathbb{Z}/N\mathbb{Z})[x]/R_{m_1}$. By taking $Q_n = {(x^e)}^n$ in $R$, we can compute a polynomial of degree $6$ such that $Q_n(m_1) = {(m_1^e)}^n = p_1^n$ modulo $N$; and then I stopped there, completely blind to the fact that the solution was right there.
8 minutes before the competition, I realised we can work in $R$ to find a polynomial with root $p_1 = m_1^e$ by solving for a linear combination (in $\mathbb{Z}/N\mathbb{Z}$) of $Q_1, Q_2, Q_3…, Q_6$ such that the result is a constant, which is just gaussian elimination over $M_6(\mathbb{Z}/N\mathbb{Z})$. We can then use coppersmith to solve for $p_1$! I didn't implement this idea however, as I thought I had more chance solving Disk (I did, but I didn't solve it anyways).
After the competition, the admins released the challenges for the finals to those who participated in the quals. Within 2 hours, fellow SEE team member @Neobeo solved this challenge and sent his solution to the chat. I hence directly copy his solution as implementation for the above described idea:
Disc
- Category: Misc
- Flag:
grey{Ain't_the_plot_looks_amazing?xqK!PV4Po^tCVGeg!usz}
We are given a single 32mb text file with a list of coordinates. That's all.
1
2
3
4
5
6
7
8
1.0476055457521123 -5.913929203203956
4.583149851335183 0.7111831270538542
-6.061253651968359 1.1097063424615103
2.4538683337842153 -5.376488649709055
3.776226969928298 -1.7970069202944412
4.271956234691409 2.5005779189781085
2.887218757992802 -1.7068344511095725
...
Here for the actual challenge file.
I had essentially solved this challenge but I didn't get the flag since I didn't realised I had already solved it. It was a fun challenge but was pretty badly designed as the last few steps were incredibly guesswork heavy (and didn't really follow actual physical implementation) and there were many tiny things the author could have done to hint to the player that they are in the right direction.
Solution
So the first thing you'd do when you see a bunch of points is obviously to scatter plot it.
1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt
data = open("data", "r").read()
data = [(*map(float, i.split(' ')),) for i in data.split("\n")[:-1]]
data = np.array(data)
plt.scatter(data[:,0], data[:,1], s=0.001)
plt.show()
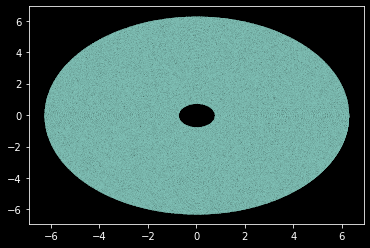
Huh a disc? Let's do a polar plot:
1
2
3
4
5
6
from numpy import exp, abs, angle
zdata = [x + y*1j for x,y in data]
plt.figure(figsize=(20,20))
plt.scatter(abs(zdata), angle(zdata), s=0.005)
plt.show()

Ohh those look like tracks like those on CDs! Let's sort them into bins based on which track they belong to, and plot to make sure we got it all right:
1
2
3
4
5
6
7
8
9
10
11
12
zdata_sorted = sorted(zdata, key=lambda x: abs(x))
diff = 0.012
intervals = np.linspace(0.75, 6.282, num=461)
bins = [[] for _ in range(462)]
for d in zdata_sorted:
idx = int(round((abs(d) - 0.75) / 0.012))
bins[idx].append(d)
for i in bins[-20:]:
plt.plot(abs(i))
plt.show()
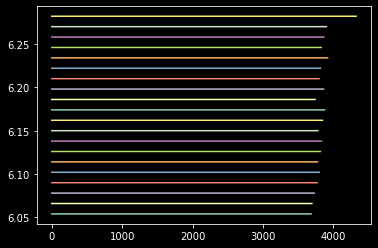
Now let's try to recover the bits from each track. But we need to also need to know the correct angle each bit spans. Let's compute that and plot to make sure it makes sense:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from collections import Counter
bins_sorted = [sorted(b, key=lambda x: angle(x)) for b in bins]
_bins_angle_diff = []
for i in range(len(bins_sorted)):
owo = angle(bins_sorted[i])
owo = set([owo[i+1] - owo[i] for i in range(1, len(owo)-1)])
_bins_angle_diff.append(min(owo))
init_adiff = 0.0068 # Manually analysed
bins_angle_diff = [(init_adiff*0.75) / (0.75 + idx*diff) for idx in range(462)]
import matplotlib.pyplot as plt
plt.plot(bins_angle_diff)
plt.plot(_bins_angle_diff)
plt.show()
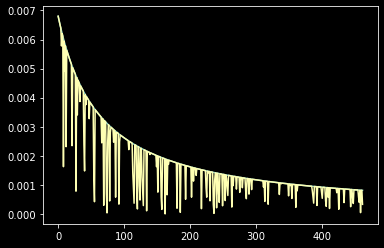
Now we can get the location of the bumps!
1
2
3
4
5
6
7
8
9
10
11
12
import math
all_owo = []
for idx in range(len(bins_sorted)):
adiff = bins_angle_diff[idx]
owo = angle(bins_sorted[idx])
owo = set([int(round((i+math.pi)/adiff)) for i in owo])
owo = [1 if i in owo else 0 for i in range(max(owo)+1)]
all_owo.append(owo)
print("".join(map(str, all_owo[0])))
# > 1110010100011100110000110110100001111011000000101010011111000001011001110011001110101010010011001110001010111110001001100101010000101011110101011100001110111111000010011100111000010000001101000110001010110010100001010100011110111010111110010000010101100110111000111011110000111110000001011000001011011101101101001101001101011111111000101000111000001000000111011000111101001110011000110001011110100101001110000100000111001000100110110101010110101000101111100001001111100000100100101111000000000100001000101101100011110100010011011011001011001000101000010001101011011010000011011001010101001000110110001001101011010011100100011001001110010100000100000010111001000111000100011011010111011011000110101101100100011111100111100101001101101001111011010010000101000111111000101011111010010010011011011111010011101101100100001111000101111001100010001001001111000100010100001100101111110001111111011100001101110110110100110011100011
Huh those bits don't look like ascii to you do they?
Okay it took me about 45 minutes to get here. I spent the next 5 hours fucking around with the bits and researching on the numerous ways bits get encoded on a disc. THIS is where my enjoyment with this challenge rapidly went downhill. In case you haven't suspected, THIS CHALLENGE HAS ALREADY BEEN SOLVED. But before I reveal that, here's why I ended up hating this challenge:
First off, on an actual CD, when there's no change in bumps, like 1->1 or 0->0, it indicates a 0 bit. Likewise, if there's a change, it indicates a 1. Furthermore bytes are encoded on a CD in a rather messy way in order to solve the physical challenges of reading from a disc. I've even tried Eight-to-fourteen modulation in the hopes to get some plaintext.
Unfortunately, this challenge encoded a 1 as a bump and 0 as no bump, which is completely different from what happens physically. In addition, bytes are simply encoded as ASCII; HOWEVER, most of the data is random trash and the flag is just placed somewhere in the middle.
In other words, the bits I showed above, if I decoded all the tracks, I would have gotten the flag. Unfortunately, nothing in the challenge indicated this as such, and I wasted precious 5 hours in this CTF going completely off course. What the author could have done, is to not just put random trash bytes, but maybe gibberish ascii characters in order to at the very least reduce the amount of guesswork this challenge already demands.
Whatever, here's the final part of the solution. You need to bruteforce the bit alignment to whatever whatever ugh
1
2
3
4
5
6
7
8
9
10
11
12
13
write = b""
for owo in all_owo:
for j in range(8):
bowo = "".join(map(str, owo))[::-1]
bowo = [int(bowo[8*i+j:8*i+8+j], 2) for i in range(len(bowo)//8)]
write += bytes(bowo)
bowo = "".join(map(str, owo))
bowo = [int(bowo[8*i+j:8*i+8+j], 2) for i in range(len(bowo)//8)]
write += bytes(bowo)
import re
print(re.findall(b"grey{.+}", write)[0].decode())
# > grey{Ain't_the_plot_looks_amazing?xqK!PV4Po^tCVGeg!usz}
